层次聚类: 从原理到应用

探索性数据挖掘的关键技术之一是聚类-基于某种相似性度量将点分为不同的组。

我们可以通过欧几里得距离，曼哈顿距离（坐标之间的绝对差之和）和马哈拉诺比斯距离（与标准差的均值之差）或通过皮尔逊相关或斯皮尔曼相关来估计两个数据点之间的相似性。

聚类分析时，我们的主要目标是获取数据分组，其中：

• 每个组（$C_i$）都是训练数据（U）的子集：$C_i \subset U$
• 所有集合的交集为空集合：$C_i \land C_j = 0$
• 所有分组的并集等于训练数据：$C_i \lor C_j = U$

层次聚类工作过程

当然这是理想的状况。我们很少获得分离如此清晰的数据。聚类数据最简单的技术之一就是层次聚类。首先，我们从 2D 图中获取一个点。现在我们要找到它的最近邻居。最近的邻居当然取决于我们选择的距离的度量，但是现在就开始使用欧几里得距离，因为它最容易可视化。

第一步就是找到最近的点:

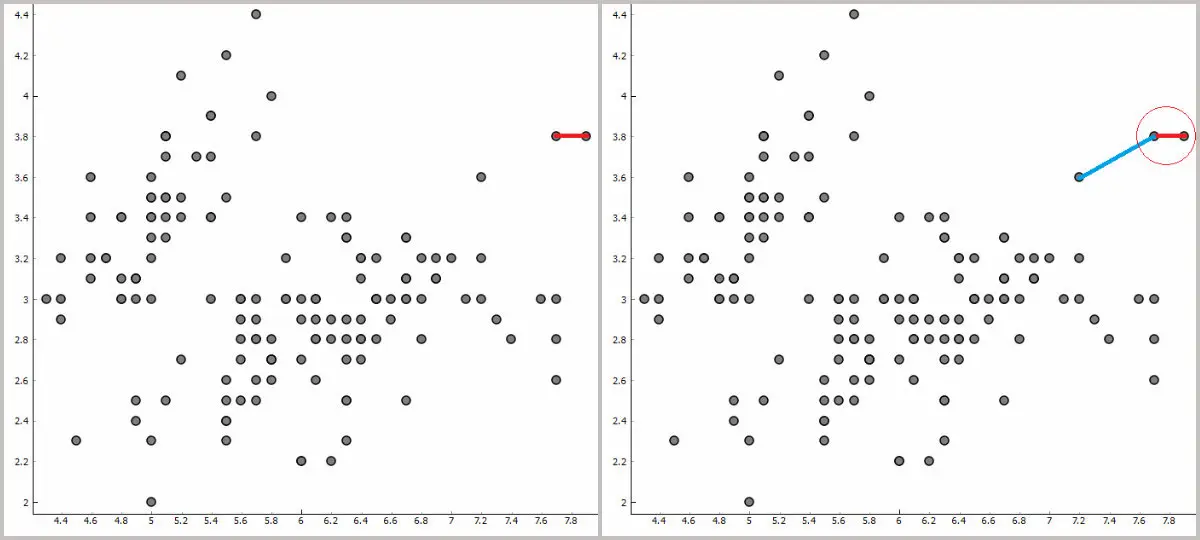
欧几里得距离计算:

自然，距离越短，两个点越相似。最初，所有点都位于各自的特定簇(或者叫聚类)中。然后我们寻找图中每个点的最接近点。我们固定最接近的点，并将原始点和最接近的点组成一个簇。现在，我们再次重复该过程。找到最接近我们新簇的点 –> 将其添加到簇 –> 查找最近的点。我们重复此过程，直到将所有点分组到一个簇中。

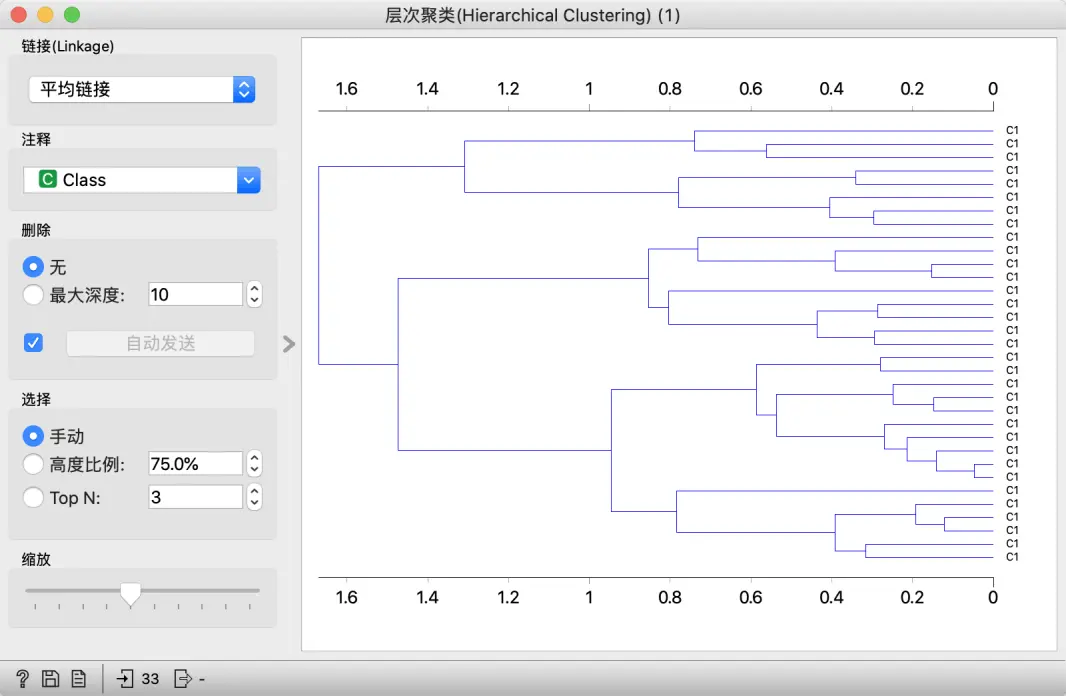
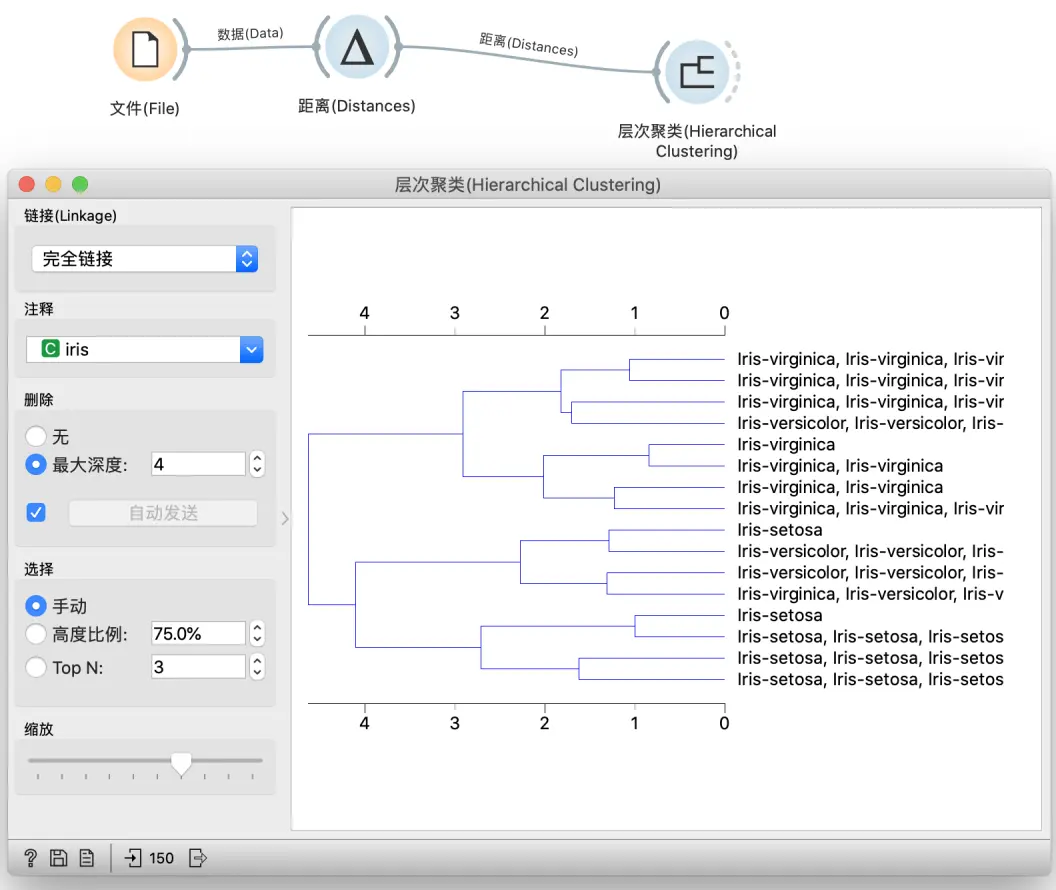
此过程的可视化称为树状图，这是层次聚类小部件中显示的内容。

计算距离

要考虑的另一件事是，当聚类中已有两个或更多点时，点之间的距离。我们要选择簇中最接近的点还是最远的点？

• 图A 显示到最接近点的距离 – 单链接。
• 图B 显示到最远点的距离 – 完全链接。
• 图C 显示簇所有点的平均距离 – 平均链接。

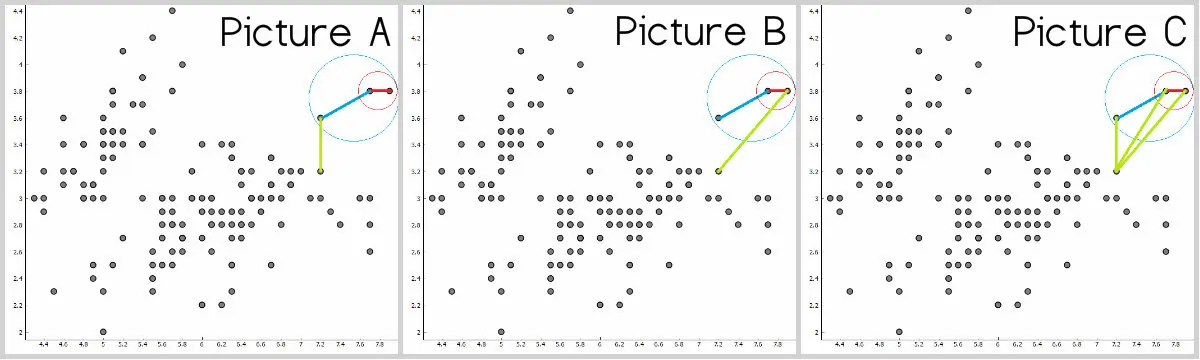
即使凭直觉，单链接的缺点也是会产生拉长的拉伸簇。如图所示工作流, 如果我们想要分开 “双C” 数据需要怎么设置呢?

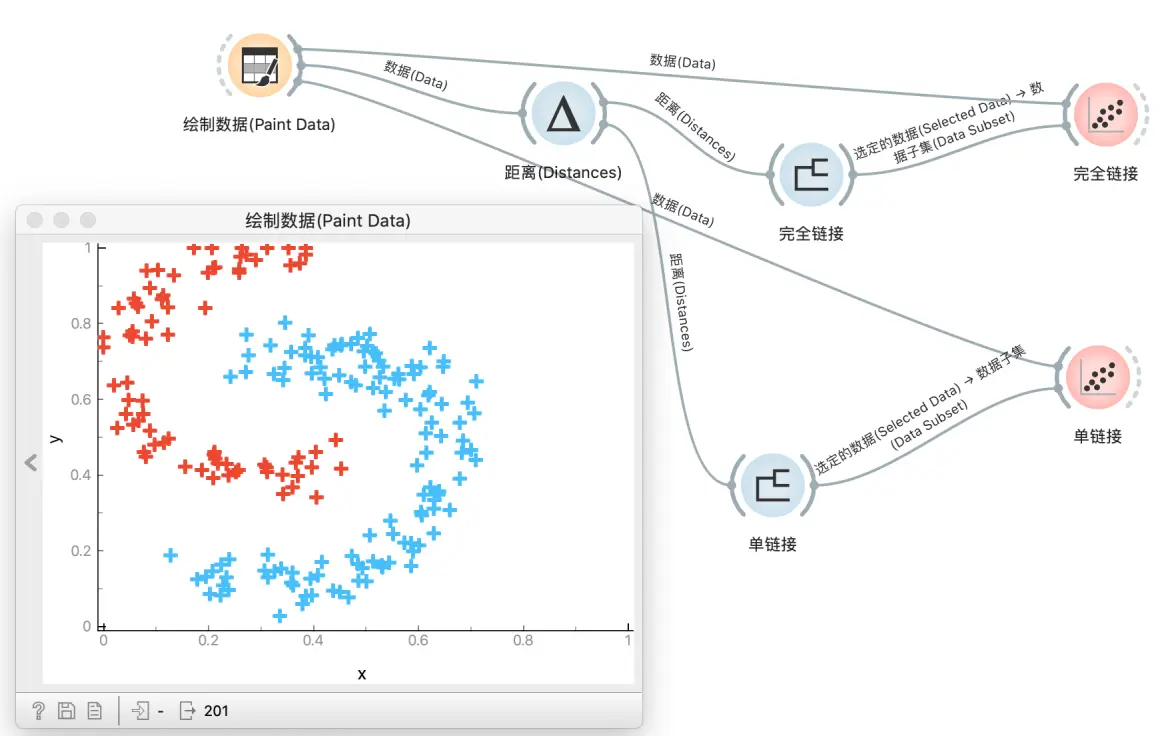
通过理论和实验都能告诉我们, 如果想把二者分开, 使用单链接是更好的选择.

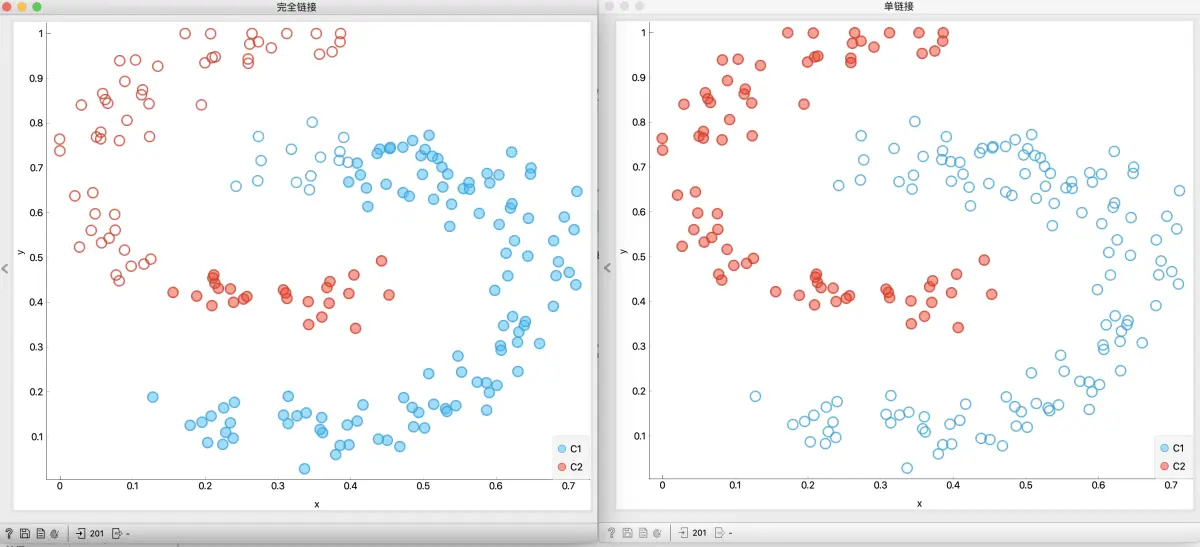
但是如果认为红色 C 顶部的点与红色 C 下部的点完全不同, 那么完全链接在此效果更好，因为它很好地使群集居中。 但是，完全链接的缺点是离群值太多了。

自然，每种方法都有其优点和缺点，因此最好了解它们的工作方式以正确使用它们。

一个额外的提示：单链接对于图像识别非常有用，因为它可以跟踪曲线。

关于层次聚类，我们还有很多要说的，但总而言之，让我们说明一下这种方法的优缺点：

• 优点：汇总数据，适用于小型数据集
• 缺点：计算量大，在较大集合上失败

下载本工作流

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里