损失函数

如何知道一个模型是否好呢? 我们可以使用损失函数

概述

损失函数描述的是每个实际值与对应预测值的差异. 它可以看做是老师对考试卷错题扣除的分数，错题越多扣分越多。

损失函数有很多种类, 但是不管什么种类, 他们只是对扣除分数采用不同方法计分，也是错题越多扣分越多, 但是具体扣除多少分视不同损失函数而定。正因为它们都是计量扣分的，也就是相对满分答卷的损失，所以叫做损失函数。顾名思义，损失函数应该其值越小越好。

回归问题的损失函数

什么是回归问题

均方差 (MSE)

均方差 (MSE) 损失一般是回归问题的默认损失。也是经常说的L2损失

在数学上，如果目标变量的分布为高斯分布，则是在最大似然推理框架下的首选损失函数。它是首选的损失函数，只有在有充分理由的情况下才会更改为其他损失函数。

均方差是预测值 ($\hat{y_i}$) 与实际值 ($y_i$) 之间平方差的平均值:

\[\dfrac {1}{m} \Sigma{(y_i - \hat{y_i})^2}\]

如下图所示, $y_i - \hat{y_i}$ 绝对值为边做正方形, $y_i$ 与 $\hat{y_i}$ 相差越大, 正方形面积越大, 正方形面积就是 $(y_i - \hat{y_i})^2$. 从图可见, 相差不太大的$y_i$ 与 $\hat{y_i}$, 会导致相差很大的正方形面积, 这就是平方导致的, 所以说均方差更多地惩罚较大的错误.

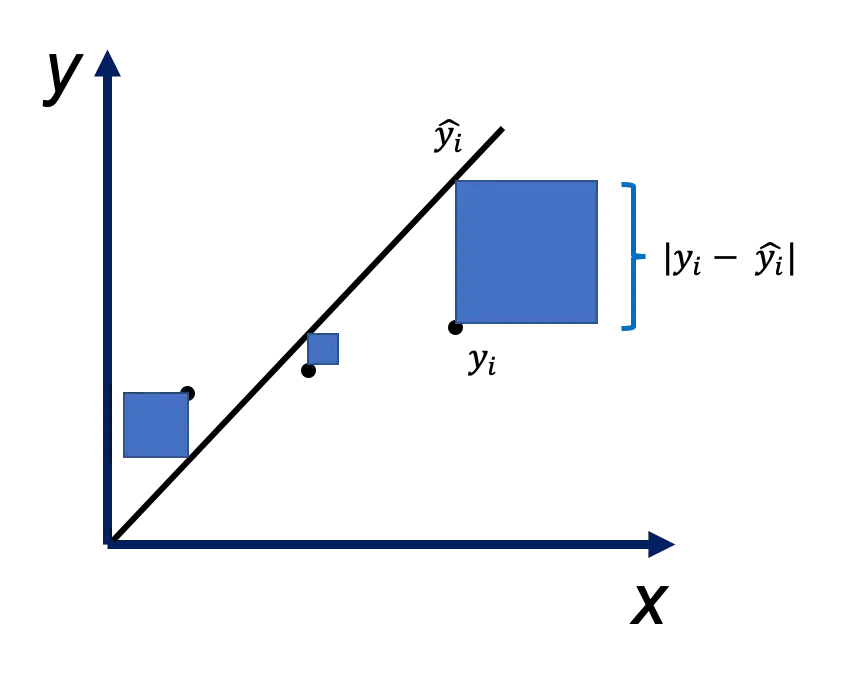
无论预测值和实际值的符号如何，结果始终为正，理想值为 0.0。平方意味着较大的错误 (即 $y_i - \hat{y_i}$ 绝对值较大) 会比较小的错误 (即 $y_i - \hat{y_i}$ 绝对值较小) 导致更多的损失，这意味着模型更多地惩罚较大的错误。

均方对数误差 (MSLE)

想象一下你是一个穷学生, 每个月只有 100 块钱的零花钱, 生活捉襟见肘. 有一天走在路上, 你丢了 10 块钱, 你有多么痛苦? 或者说你损失了 10 块钱, 你感觉你遭受了多大的惩罚? 用 MSE 解释一下? 在想象一下你是一个亿万富翁, 有一天丢了 100 块钱, 你难受吗? 或者说你损失了 100 块钱, 你感觉你遭受了多大的惩罚? 用 MSE 解释一下?

很显然, 两种情况的感觉不一样, 而且损失 10 块钱感觉比 100 块钱更痛苦. 用 MSE 解释一下? 没法解释! MSE 只会告诉你 100 块的损失肯定更痛苦, 但是这显然不对啊, 怎么办?

来, 了解一下均方对数误差

有些回归问题中，其目标值很分散，并且在预测很大的值时，可能不希望像均方差那样对模型进行严厉的惩罚, 或者说对绝对损失值进行惩罚, 而是希望惩罚相对损失,即:

\[\dfrac {1}{m}\Sigma(\dfrac {y_i+1}{\hat{y_i}+1})^2\]

$+1$ 为了防止出现 0 而无法计算

为了方便计算, 我们希望写成 $a - b$ 类似的形式, 如何做到呢? 用 $\log$, 所以上式写成:

\[\dfrac {1}{m} \Sigma (\log\dfrac {y_i+1}{\hat{y_i}+1})^2\]

因为 $\log(a/b)$ 可以写成 $\log a - \log b$, 所以上式可以写作:

\[\dfrac {1}{m} \Sigma (\log(y_i+1) - \log(\hat{y_i}+1))^2\]

这就是均方对数误差损失 (Mean Squared Logarithmic Error Loss, MSLE)。它其实就是先计算每个预测值和真实值的自然对数，然后计算二者均方差。它可以减弱较大预测值误差的惩罚效果。

当模型直接预测未缩放的数量时，它可能更合适。

如果只能用 MSE 但是想用 MSLE 怎么办? 先把目标取 log 就可以了

均方根误差 (RMSE) 和均方根对数误差 (RMSLE)

MSE 和 MELE 有一个问题是它们都做了平方。由于我们的数据的阶数为1，而这两个损失函数阶数为2，因此，我们无法将数据与错误直接相关联。因此，我们可以采用将二者再取平方根的方法.

这样就有了均方根误差 (RMSE):

\[\sqrt {\dfrac {1}{m} \Sigma{(y_i - \hat{y_i})^2}}\]

还有就是均方根对数误差 (RMSLE)

\[\sqrt {\dfrac {1}{m} \Sigma (\log(y_i+1) - \log(\hat{y_i}+1))^2}\]

平均绝对误差 (MAE)

在某些回归问题上，目标变量的分布可能大部分是高斯分布，但可能有离群值，例如远离平均值的过大或过小值。

在这种情况下，平均绝对误差(Mean Absolute Error Loss, MAE) 损失是一种适当的损失函数，因为它对异常值更为稳健。它也常被称作L1损失

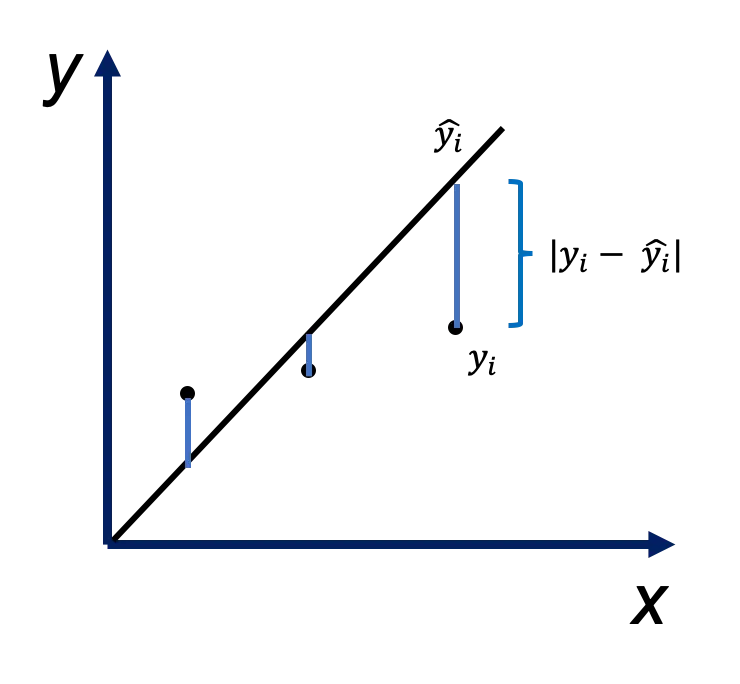
它为实际值和预测值之间的绝对差的平均值:

\[\dfrac {1}{m} \Sigma{|y_i - \hat{y_i}|}\]

使用 MSE 更容易求解，但使用 MAE 对离群点更加稳健

如果离群点是会影响业务、而且是应该被检测到的异常值，那么我们应该使用MSE。另一方面，如果我们认为离群点仅仅代表数据损坏，那么我们应该选择MAE作为损失。

更多 MSE 与 MAE 比较, 请查阅 L1 vs. L2 Loss function

Huber Loss，平滑的平均绝对误差

L1损失对异常值更加稳健，但其导数并不连续，因此求解效率很低。L2损失对异常值敏感，但给出了更稳定的闭式解（closed form solution）（通过将其导数设置为0）

两种损失函数的问题：可能会出现这样的情况，即任何一种损失函数都不能给出理想的预测。例如，如果我们数据中90％的观测数据的真实目标值是150，其余10％的真实目标值在0-30之间。那么，一个以MAE为损失的模型可能对所有观测数据都预测为150，而忽略10％的离群情况，因为它会尝试去接近中值。同样地，以MSE为损失的模型会给出许多范围在0到30的预测，因为它被离群点弄糊涂了。这两种结果在许多业务中都是不可取的。

在这种情况下怎么做？一个简单的解决办法是转换目标变量。另一种方法是尝试不同的损失函数。这是我们的第三个损失函数——Huber Loss——被提出的动机。

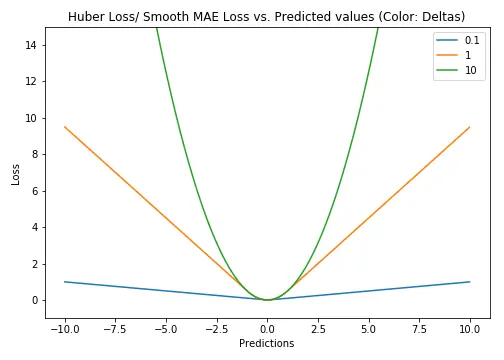
Huber Loss对数据离群点的敏感度低于平方误差损失。它在0处也可导。基本上它是绝对误差，当误差很小时，误差是二次形式的。误差何时需要变成二次形式取决于一个超参数，$\delta$(delta)，该超参数可以进行微调。当 $\delta \approx 0$时， Huber Loss 接近 MAE，当 $\delta \approx \infty$（很大的数）时，Huber Loss 接近 MSE。

\[L_{\delta }(y,\hat{y_i}|)={\begin{cases}{\frac {1}{2}}(y_i-\hat{y_i}|)^{2}&{\textrm {for}}|y_i-\hat{y_i}||\leq \delta ,\\\delta \,|y_i-\hat{y_i}||-{\frac {1}{2}}\delta ^{2}&{\textrm {otherwise.}}\end{cases}}\]

$\delta$ 的选择非常重要，因为它决定了你认为什么数据是离群点。大于 $\delta$ 的残差用 L1 最小化（对较大的离群点较不敏感），而小于 $\delta$ 的残差则可以“很合适地”用 L2 最小化。

分类问题的损失函数

什么是分类问题

二元交叉熵

交叉熵 (Cross-Entropy Loss) 是用于二元分类问题的默认损失函数。它适用于二进制分类，其中目标值在集合{0，1}中。

在数学上，它是最大似然推理框架下的首选损失函数。只有在有充分理由的情况下才不使用此损失函数。

\[L=-[y\log \hat y + (1-y) \log (1-\hat y)]\]

对于二分类问题，目标只会取 0 或者 1。这个损失函数是什么意思呢？为什么它可以作为损失函数呢？我们可以将它分情况考虑。当真实值 y 是 0 时，交叉熵变为了:

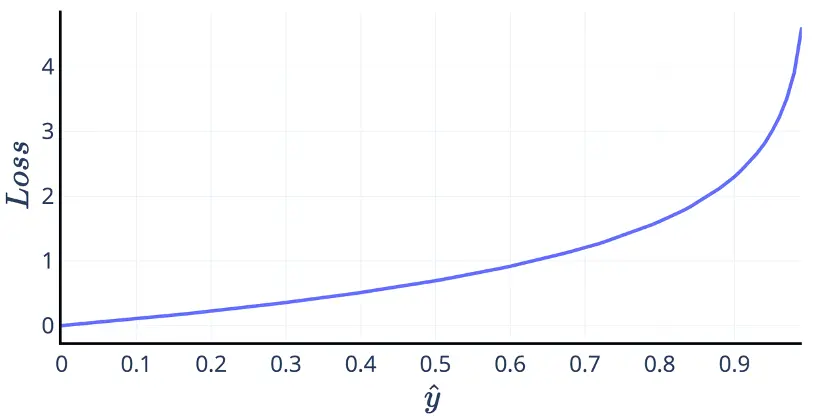
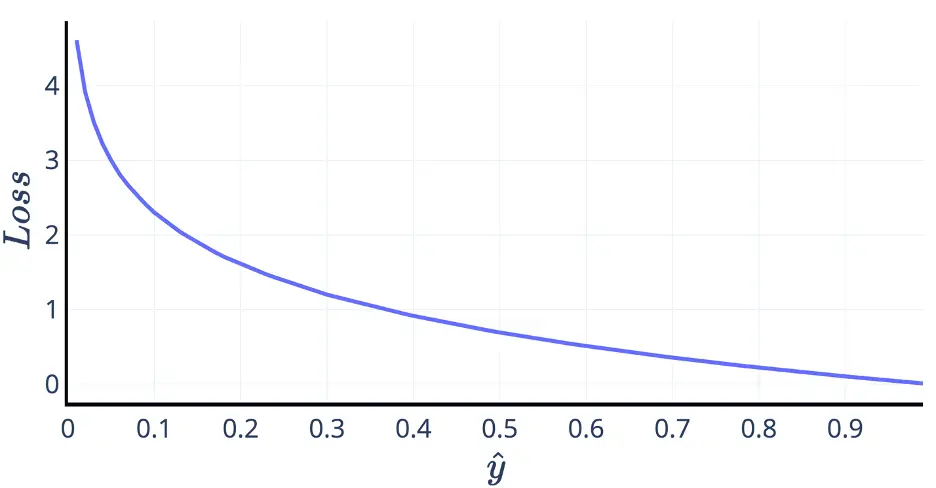
\[L=-\log(1-\hat{y})\]

预测值 $\hat{y}$ 是一个取值范围为 [0,1] 的概率，这样交叉熵就成了下图的样子。想要最小化这个损失函数，必然想要预测值越接近 0 越好。

类似的，当真实值 y 是 1 时，交叉熵变为了:

\[L=-\log \hat{y}\]

这样交叉熵就成了如下图的样子。想要最小化这个损失函数，必然想要预测值越接近 1 越好。

多分类问题的交叉熵($\sum {y_i \log \hat{y_i}}$)与二元交叉熵思路类似, 不多介绍

Hinge Loss

二进制分类问题的交叉熵的替代方法是铰链损失函数 (Hinge Loss)，主要是为与支持向量机（SVM）模型一起使用而开发的。

它适用于目标值位于集合{-1，1}中的二进制分类。

Hinge Loss 鼓励样本具有正确的符号，当实际类值和预测类值之间的符号不同时，分配更多错误。

\[L = \max(0, 1- \hat y y)\]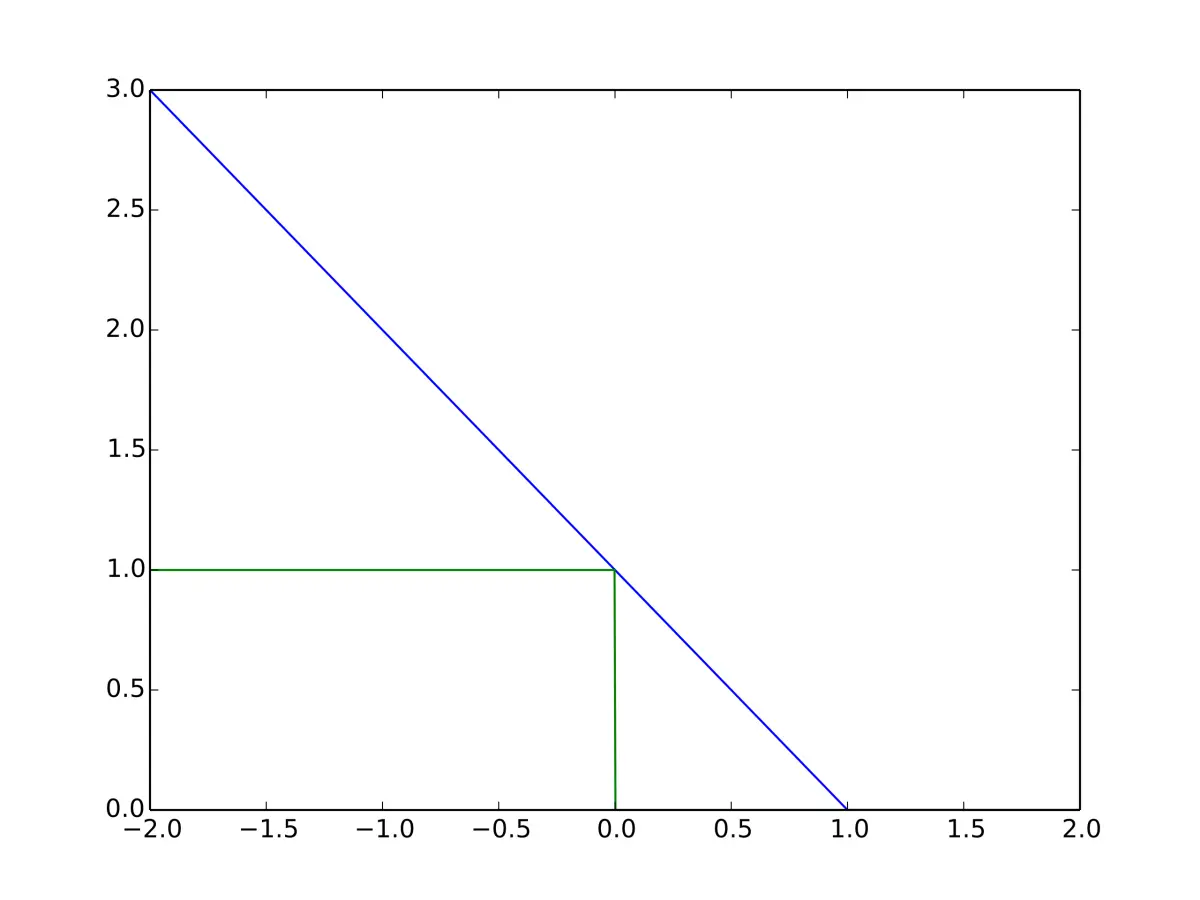

当 $\hat{y}$ 和 $y$ 同号（意即分类器的输出 $y$ 是正确的分类），且 $ |y| \ge 1 $ 时，Hinge Loss $L = 0$。但是，当它们异号（意即分类器的输出 $y$ 是错误的分类）时，$L$ 随 $y$ 线性增长。套用相似的想法，如果$|y| \le 1$，即使 $\hat{y}$ 和 $y$ 同号（意即分类器的分类正确)，但是间隔不足，仍然会有损失。

关于 Hinge Loss 的性能意见不统一，在二元分类问题上比交叉熵的性能有时更好有时更差。

参考文献

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里

概述