线性回归

介绍回归的基本概念，进而引出最小二乘法，最后看看如何判断拟合的好坏。

回归

统计学中，回归是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。 机器学习中，回归是一种预测性的建模技术，它研究的是特征和标记之间的关系。

下面我们以简单线性回归为例，看看回归是什么。 简单来说, 回归就是回到平均值

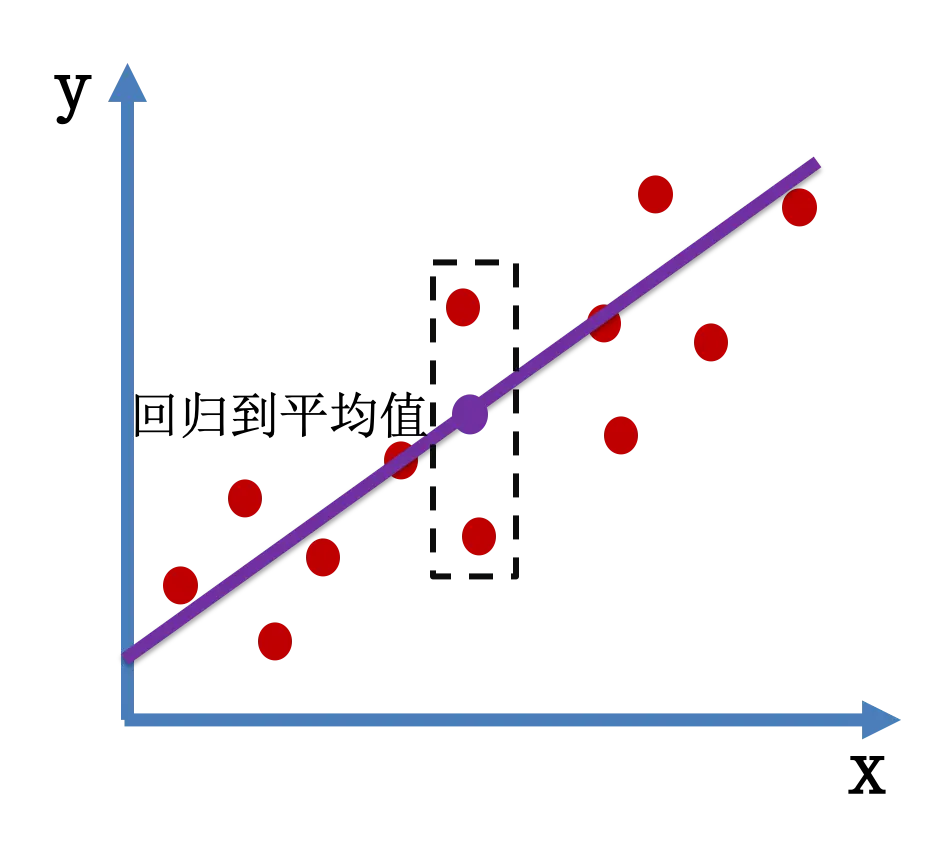
简单线性回归

简单线性回归处理的问题就是：$y = wx + b$ 的问题。在机器学习中，$y$ 是标记，$x$ 是特征，$w$是权重，$b$是偏置。简单线性回归就是通过已知的 $x$ 和 $y$ 求解未知的 $w$ 和 $b$。

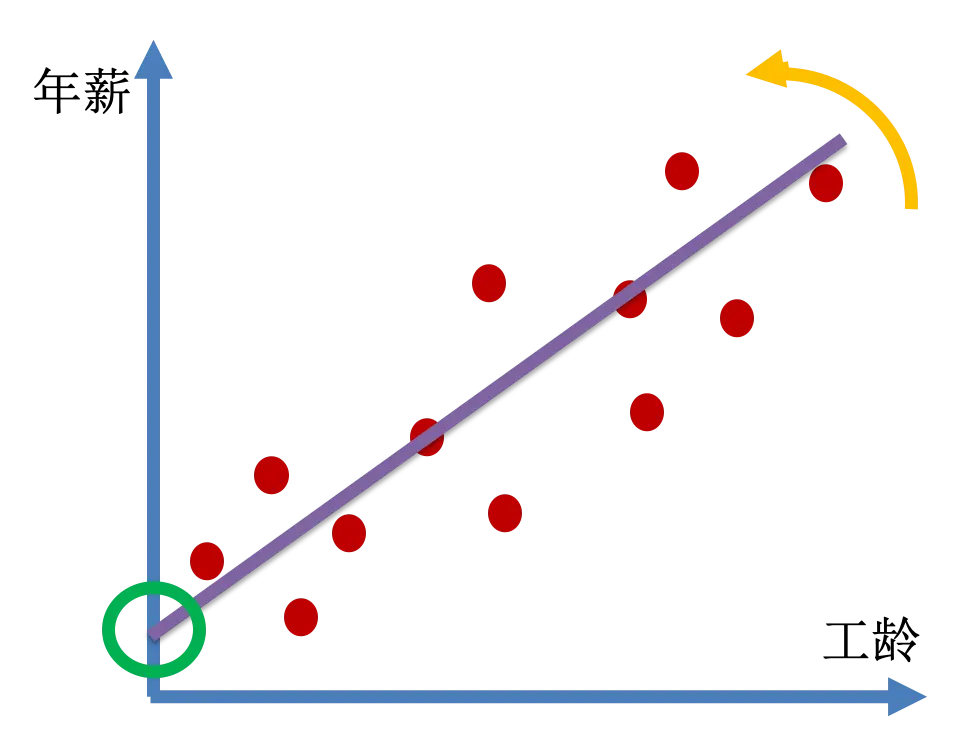
以年薪与工龄的关系为例，来看看简单线性回归的公式的意义。

偏置就是直线与纵轴的交点，权重其实就是斜率。简单线性回归就是找到合适的权重和偏置，使这条线尽可能的接近这些点的分布。

多元线性回归

和简单线性回归类似，多元线性回归的问题是：$y = b + w_1x_2 + w_2x_2 + … + w_n x_n$，他要通过已知的 $x_i$ 和 $y$ 求解未知的 $w_i$ 和 $b$

亲自动手

转到亲自动手

最小二乘法

我们已经知道了回归是要让回归线能够尽可能的接近这些点的分布，下一步问题就来了，怎么保证尽可能接近点的分布呢？我们可以用最小二乘法来解答这个问题。

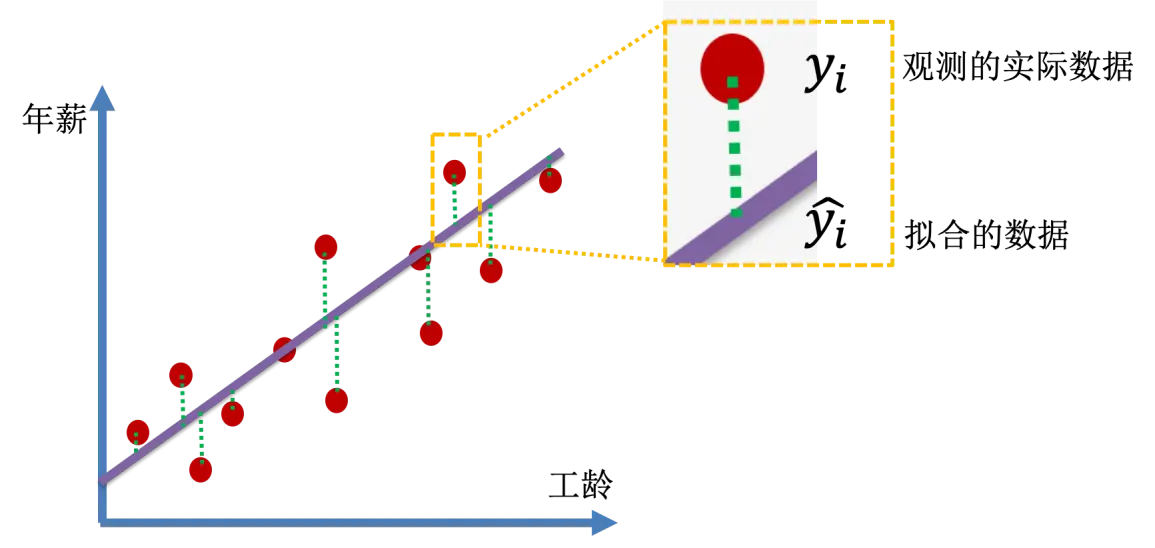
假设观测到的实际数据点纵坐标 $y_i$，从这个点作垂线，与拟合的直线交点的纵坐标记为 $\hat{y_i}$。拟合的好的话，我们可以理解为想要每一组 $y_i$ 和 $\hat{y_i}$ 尽可能的接近。但是如果采用 $y_i - \hat{y_i}$ 的话，各个观测值与拟合值差的和 $\Sigma{(y_i - \hat{y_i})}$ 会正负值互相抵消，并不能真正反映我们需要的接近程度。所以，我们采用 $(y_i - \hat{y_i})^2$ 来度量每个观测点和拟合值接近程度，它们的和 $\Sigma{(y_i - \hat{y_i})^2}$ 的大小来判断接近程度的好坏。可以看出，这个值越小，拟合程度越好，最小二乘法要做的，就是最小化 $\Sigma{(y_i - \hat{y_i})^2}$。

$\dfrac {1}{m} \Sigma{(y_i - \hat{y_i})^2}$ 就是均方差 – Mean Squared Error(MSE)，这里 $m$ 是样本数目。

判断拟合好坏

很多时候，机器学习工程师将 $\Sigma{(y_i - \hat{y_i})^2}$ 最小化之后就结束工作了。但是对于统计学家来说，还要继续判断模型的解释能力，即度量响应的变化中可由自变量解释的部分所占的比例。

决定系数

假设一组数据 $X_1, X_2, …, X_n$，我告诉了你除了 $X_n$ 以外所有的数值，让你猜猜 $X_n$ 是多少，你觉得下面那个更靠谱：

• 最大值
• 最小值
• 平均值
• 随便猜一个

相信大多数人都会觉得平均值更合适一些。如果就把这个平均值画出来，然后找到每个实际的观测点到这个平均线的距离，算出这些距离的平方和：$\Sigma{(y_i - \bar{y})^2}$，这里的 $\bar{y}$ 就是平均值。

下面我们给出两个定义：

\[SS_{res} = \Sigma{(y_i - \hat{y_i})^2}\] \[SS_{tol} = \Sigma{(y_i - \bar{y})^2}\]

上面第一个公式是残差平方和，判断了观测点和回归线接近程度，第二个公式是总平方和，判断了各个测量点和平均值的接近程度。下面，我们定义决定系数：

\[R^2 = 1 - \dfrac {SS_{res}}{SS_{tol}}\]

观察这个公式及下图，线性回归（右侧）的效果比起平均值（左侧）越好，决定系数的值就越接近于1。 蓝色正方形表示线性回归的残差的平方， 红色正方形数据表示对于平均值的残差的平方。

调整的 $R^2$

$R^2$ 可以较好的反映拟合的好坏，但是有一个小问题：随着自变量的增多，$SS_{res}$ 不会变大，导致决定系数不会变小。这是否告诉我们，模型的自变量越多越好呢？事实上，模型越复杂，模型越容易出问题，简单一些的模型才好。为了能够更公平地对比不同自变量个数的模型，我们引入调整的 $R^2$（Adjusted $R^2$）：

\[Adj \ R^2 = 1 - (1-R^2)\dfrac {n - 1}{n - p -1}\]

其中，$p$ 是自变量数目，$n$ 是样本数目。

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里