逻辑回归
使用逻辑回归解决分类问题
分类问题
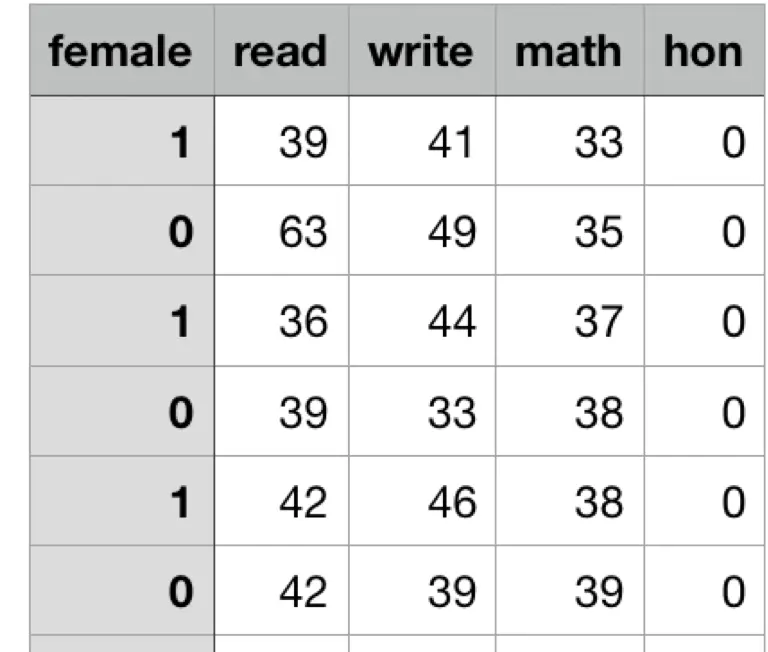
假设我想根据学生考试成绩和性别信息判断他能否获得奖学金,我们期望的结果无非两种:能或者不能。
亲自动手
转到亲自动手
从线性回归到逻辑回归
线性回归能解决吗
其中有奖标注为 $1$, 无奖标注为 $0$。假设使用回归方法解决这个问题,观察 hon(是否有奖学金) 和 read(阅读分数) 的关系:
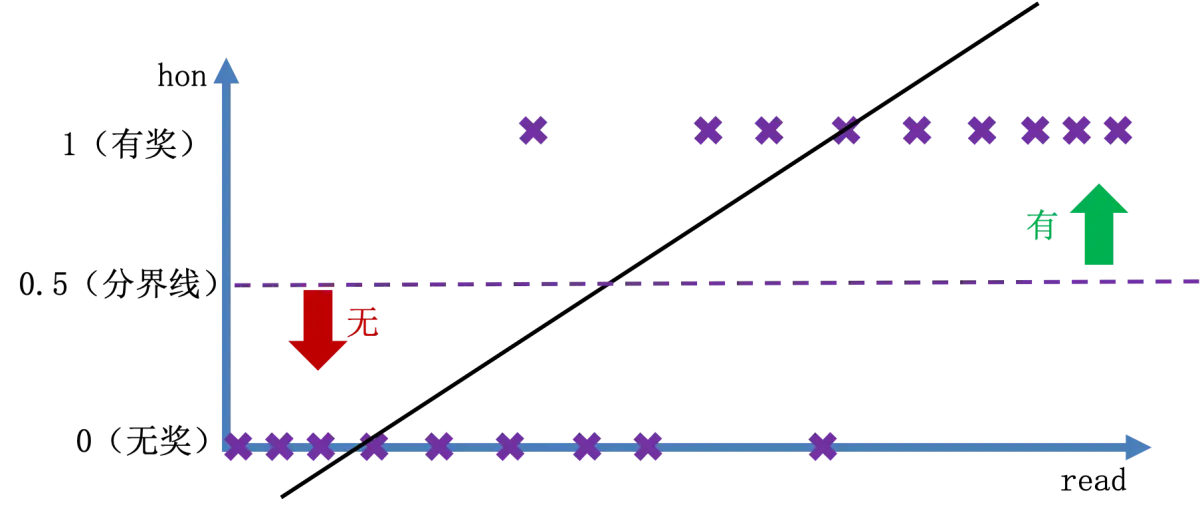
上图的斜线是回归线,回归线大于分界线 $0.5$ 的话,预测为有奖,否则预测为无奖。
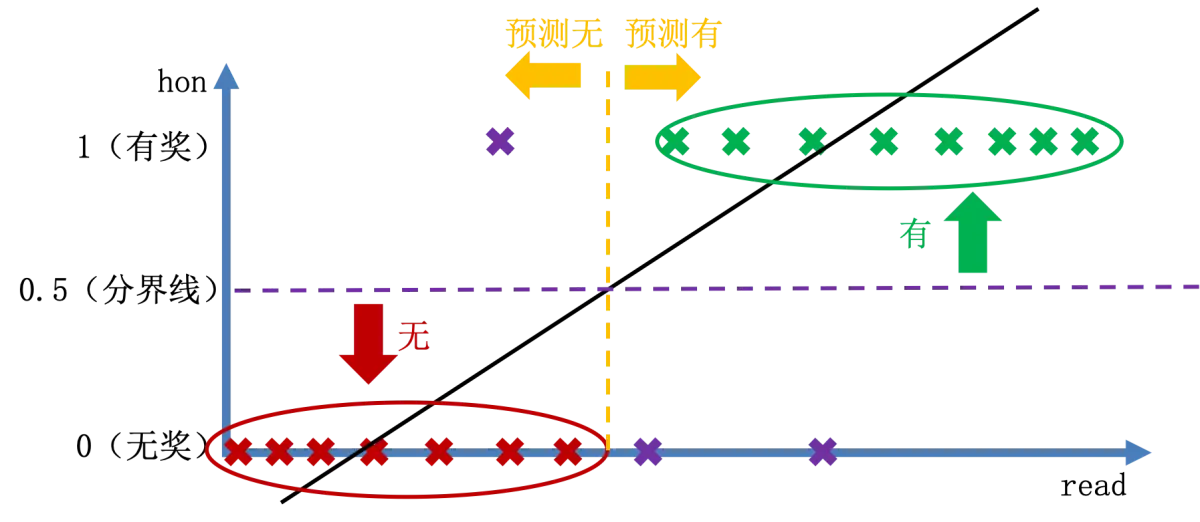
如果我们考虑将回归线值在 $0$ 和 $1$ 之间的数值考虑为能否获奖的概率,会产生了一些问题。首先,回归线预测的值大于 $1$ 怎么理解?其次,回归线预测的值小于 $0$ 怎么理解?
另外,假设右上角有一个点离得其他点很远,则为了照顾这个点,回归线将会偏离。因为一个偏离点,导致整个模型的不稳定,说明这个方法必然是存在问题的。
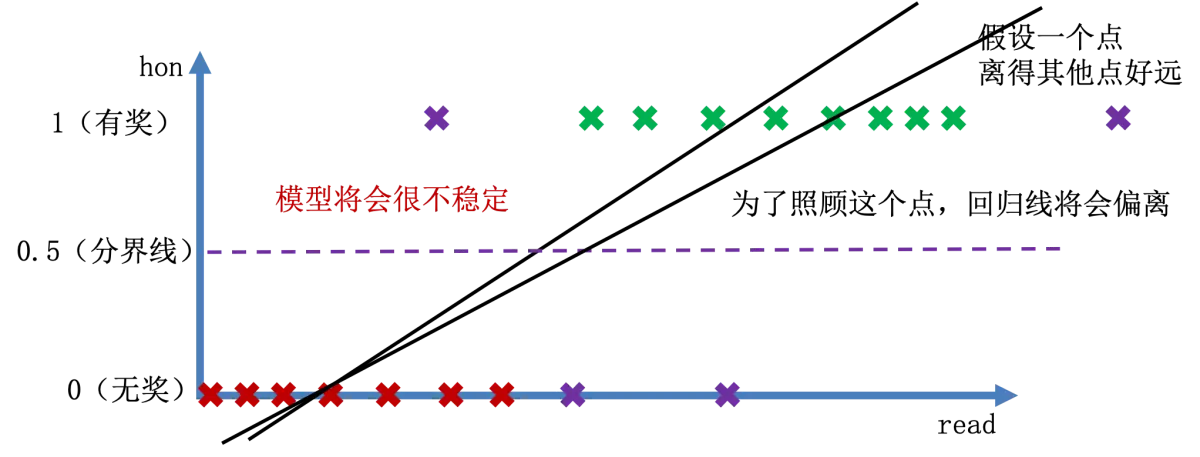
美好想象中的解决办法
为了解决这些问题,我们可以做一个美好想象,最好能做出下图这样的结果:
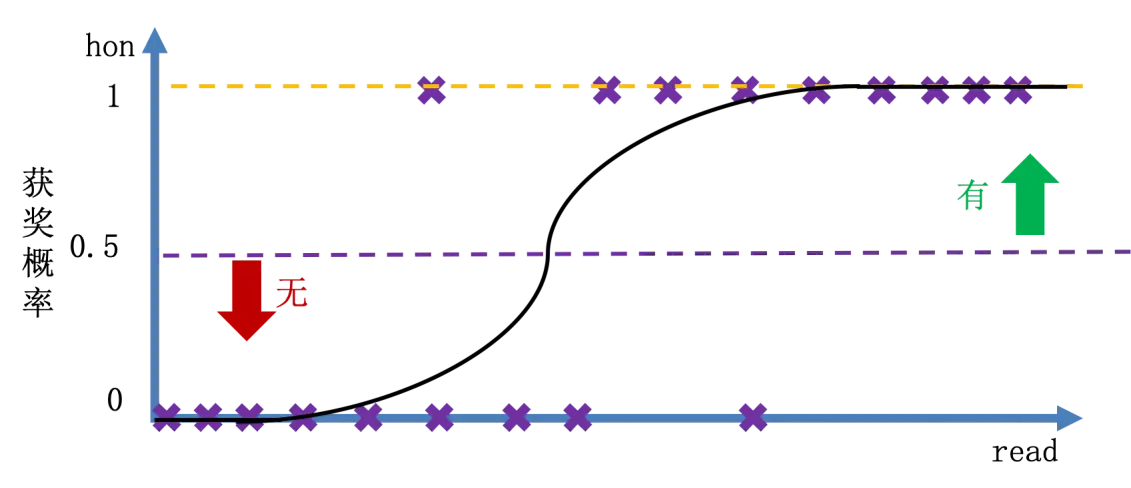
这样问题变成了如何得到上面这样的曲线。
我们使用 Sigmoid 函数将线性回归线转为逻辑回归线。Sigmoid 函数为:
\[\sigma(z) = \dfrac{1}{1+e^{-z}}\]图像为:
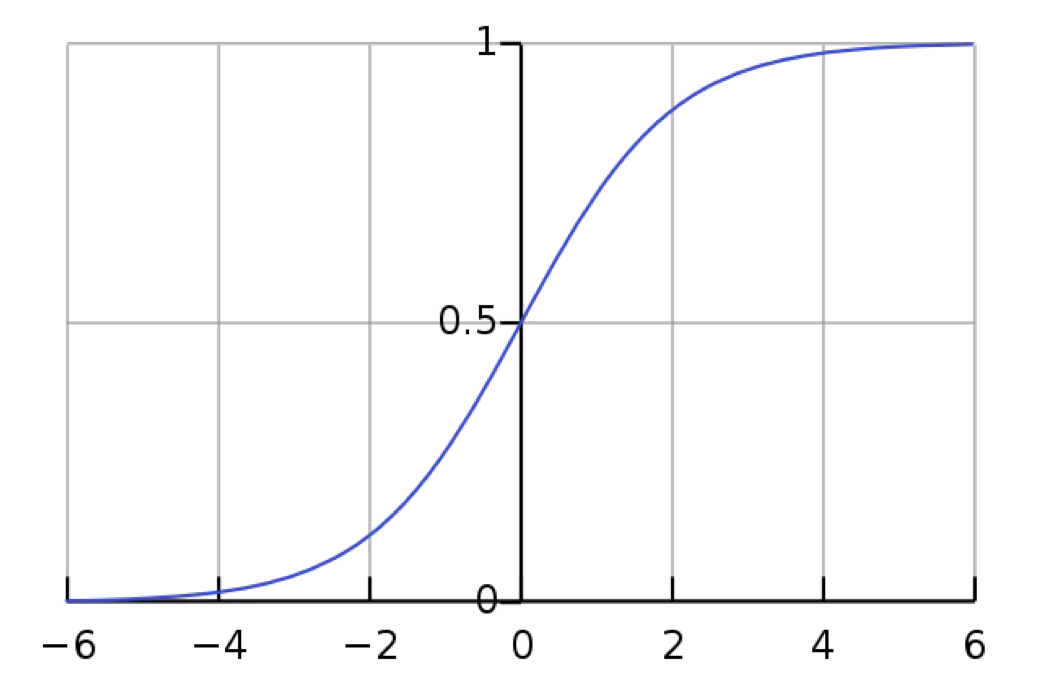
它能够将 $z = b + w_1x_2 + w_2x_2 + … + w_n x_n$ 转换为 $\hat{y}=\sigma(z)$
当 $z>0$时,$\sigma(z)>0.5$;当 $z<0$时,$\sigma(z)<0.5$。这里的 $0.5$ 就是一个分界点,也就是判定边界。
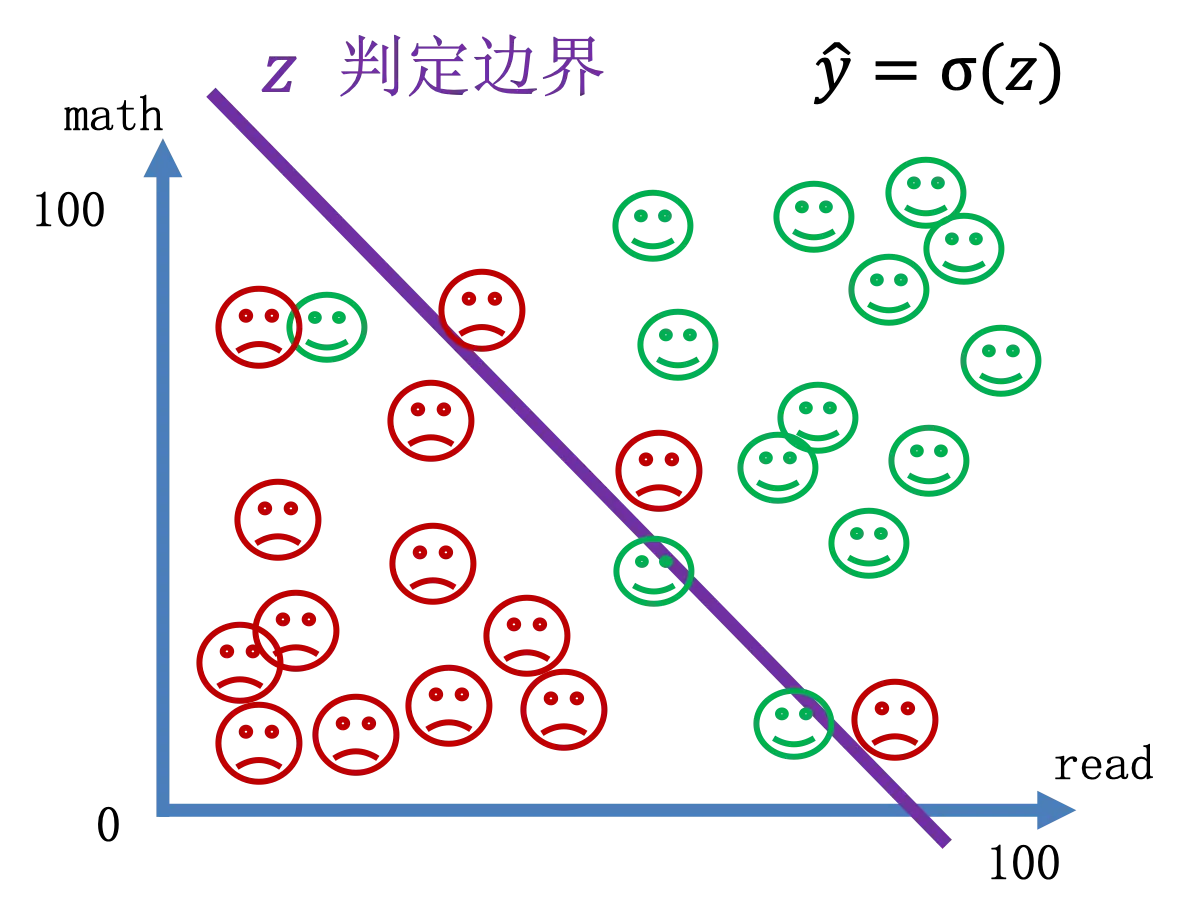
判定边界
这个例子中,线的两侧有不同的获奖预测,这条线就叫判定边界(decision boundary),我们可以调整判定边界,使得损失函数最小。
反馈问题
文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈
点我反馈进入反馈页面不知道如何反馈, 请点击这里