支持向量机
熟悉了什么是分类问题,而且用逻辑回归实际进行了分类问题的练习后,下面看看另一个重要的分类算法 – 支持向量机。
支持向量机简介
支持向量机是什么
支持向量机(support vector machine,SVM)是分类与回归分析中一种算法。给定一组训练样本,每个训练样本被标记为属于两个类别中的一个或另一个,支持向量机创建一个将新的样本分配给两个类别之一的模型,使其成为非概率二元线性分类器。除了进行线性分类之外,支持向量机还可以使用“核”技巧有效地进行非线性分类,将其输入隐式地映射到高维特征空间中。
对于支持向量机来说,数据点被视为 $n$ 维向量,而我们想知道是否可以用 $n-1$ 维超平面来分开这些点。这就是所谓的线性分类器。
三维空间中,$n=3$,则 $n-1=2$,所谓的超平面就是我们熟知的平面。类似在二维空间中,超平面其实是一条线。
简单来说,支持向量机就是找到一个超平面,使其将数据分类,并且两类数据之间的距离尽可能的大。或者更通俗地说,找一条马路作为分界线,马路越宽越好。
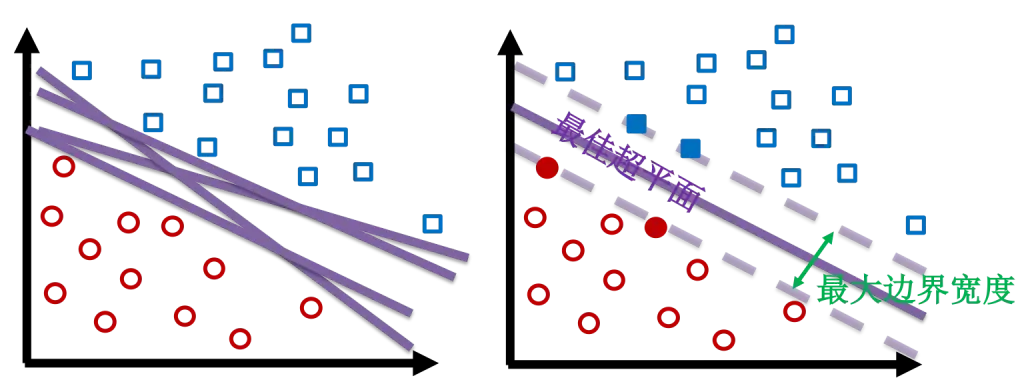
支持向量是什么
支持向量是接近超平面并影响超平面的位置和方向的数据点。但是点怎么就成向量了呢?因为每个点都可以看做是从原点出发指向此点的一个向量。使用这些支持向量作为支撑点,使边界尽可能宽。
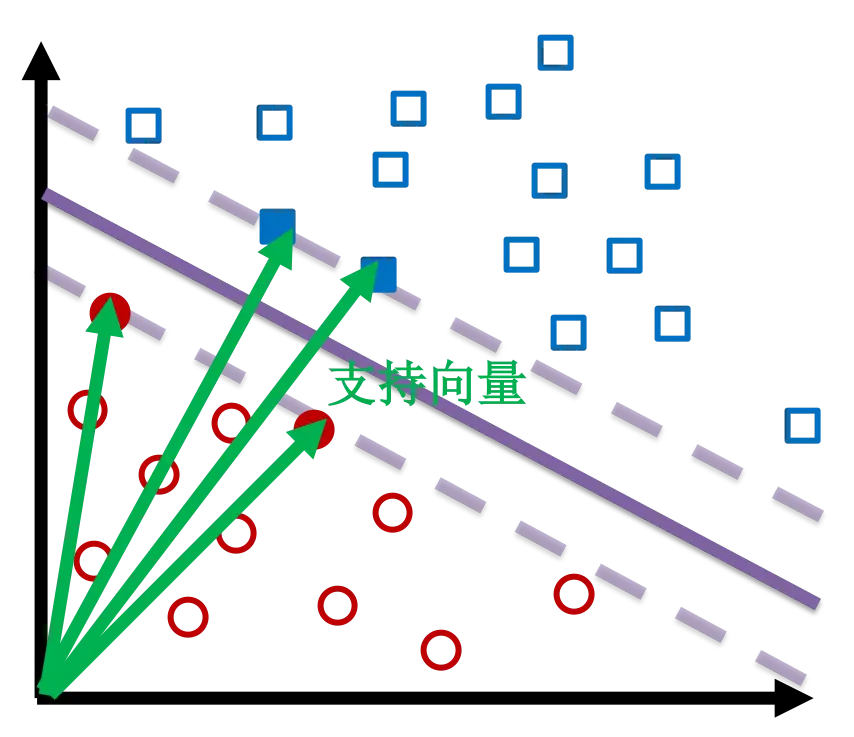
逻辑回归与支持向量机的比较
我们仅从二者的损失函数角度了解二者对数据的敏感程度的区别。其中,支持向量机使用 Hinge loss 而逻辑回归使用 Logistic loss。
这里没有考虑正则化影响。关于正则化见后面分析。
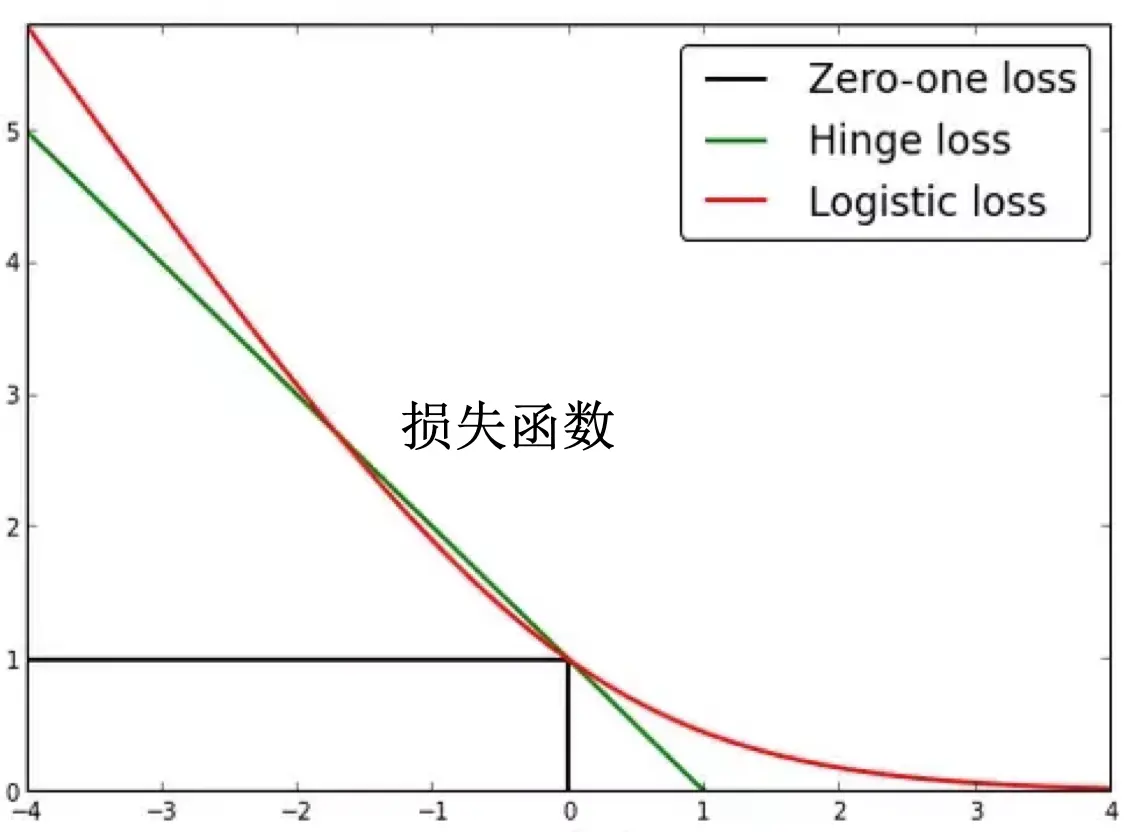
观察二者的损失函数,我们可以注意到以下四点:
- Hinge loss 没有 Logistic loss 上升的快。也就是说,Logistic loss 对于异常值会有更大的惩罚,导致逻辑回归对异常点的容忍程度相对较低。
- 不管哪个损失函数,即使分类对了,在边界附近的值也会受到惩罚,这导致二者都会要求能够更好地分类,从而使各个值能够尽可能地远离边界。
- 即使一个值被确信地分类了,也就是它离得边界很远,Logistic loss 也不会变为零。这导致逻辑回归进一步要求所有点都能够进一步远离边界。
- 如果一个值被比较好地分类了,也就是它离得边界比较远,Hinge loss 立即变为 0。这导致支持向量机并不在乎较远的点到底在哪,它只在意边界附近的点(支持向量)。在意附近的点是因为根据第二点,即使支持向量划分正确,Hinge loss 也不为 0。导致支持向量机想要将支持向量推离边界,直到 Hinge loss 为 0。
异常值(outlier)是指一组测定值中与平均值的偏差超过两倍标准差的测定值,与平均值的偏差超过三倍标准差的测定值,称为高度异常的异常值。
基于以上四点,二者的分类结果会出现以下两种显著区别:
-
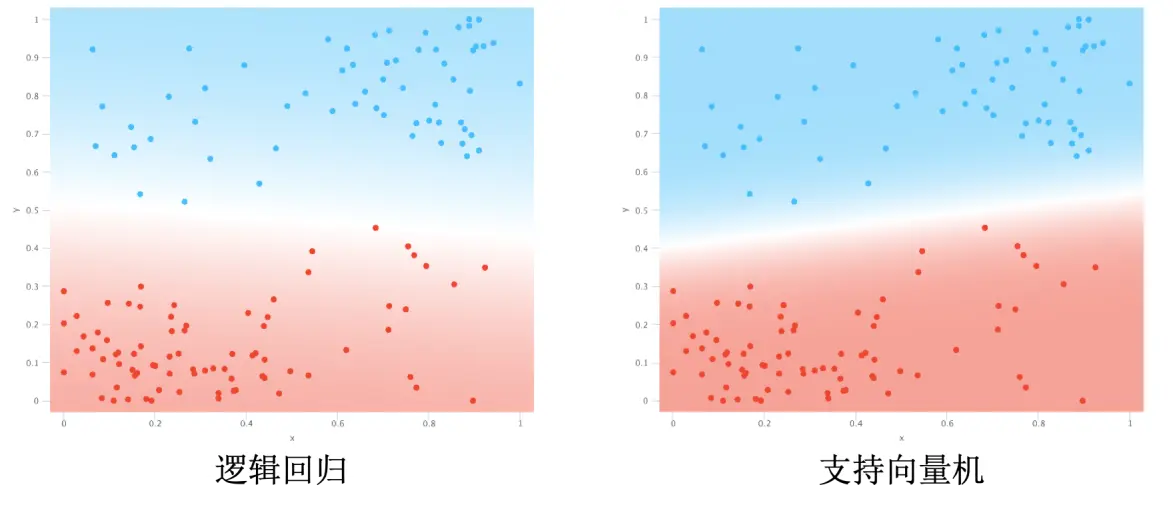
逻辑回归尽可能提高所有点分类正确的概率,而支持向量机尝试最大化由支持向量确定的边界距离。换句话说,逻辑回归尝试将所有点都远离边界;而支持向量机尝试将支持向量推得更开。
-
逻辑回归对错误的承受能力更低,它会尽可能地要求所有值都正确分类。支持向量机对错误承受能力相对较高,它的目的更多的是将边界拓宽。换句话说,逻辑回归想要的是不同种类能分开就全部分开,就算中间只有一张纸距离也算分开了;而支持向量机想要的是不同种类离得越远越好,最好是一堵厚实的墙,即使牺牲一些己类分到对方也无所谓。
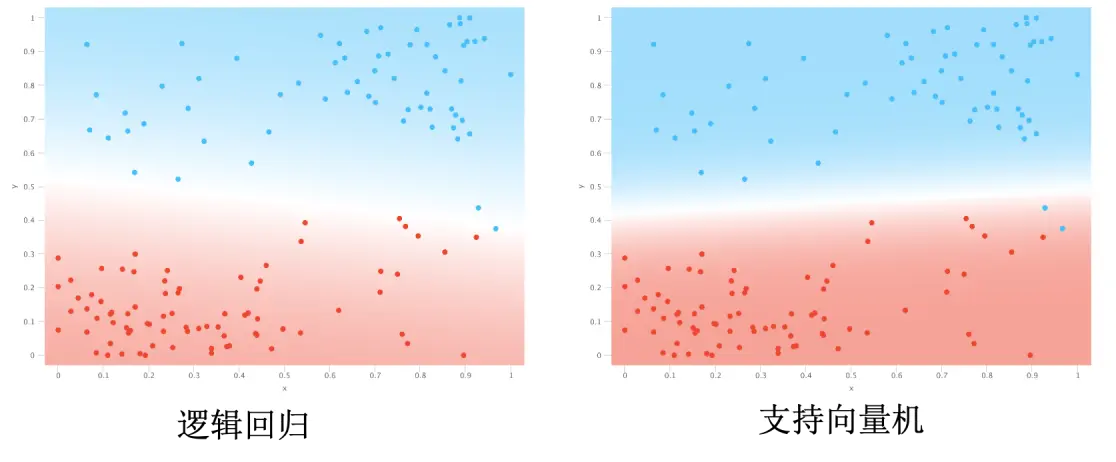
最后需要说明的是:支持向量机给出的结果就是 1 或 0,逻辑回归给出的是概率值。换句话说,逻辑回归没有给出绝对的预测,它没有帮你做决定,你需要根据概率自己去决定结果应该是 1 还是 0。而支持向量机明显帮我们做出了决定。
核
为什么使用核
前面的例子中,我们通过一条直线就可以做到比较好的分类,但是如果要分类的问题是下图所示呢?
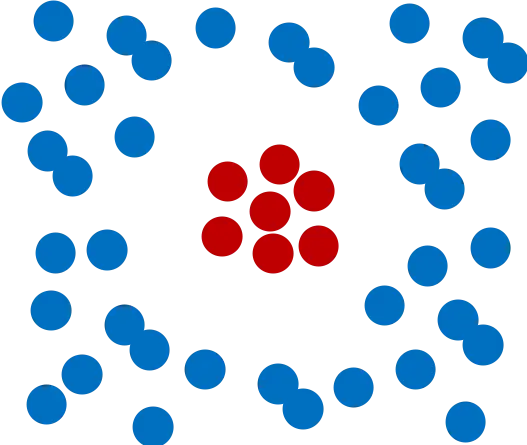
我们没办法用一条直线将二者分类。遇到这种情况怎么办呢?如果能将中间的红点提起来,是不是就可以使用一个平面作为分界面来分类了呢?
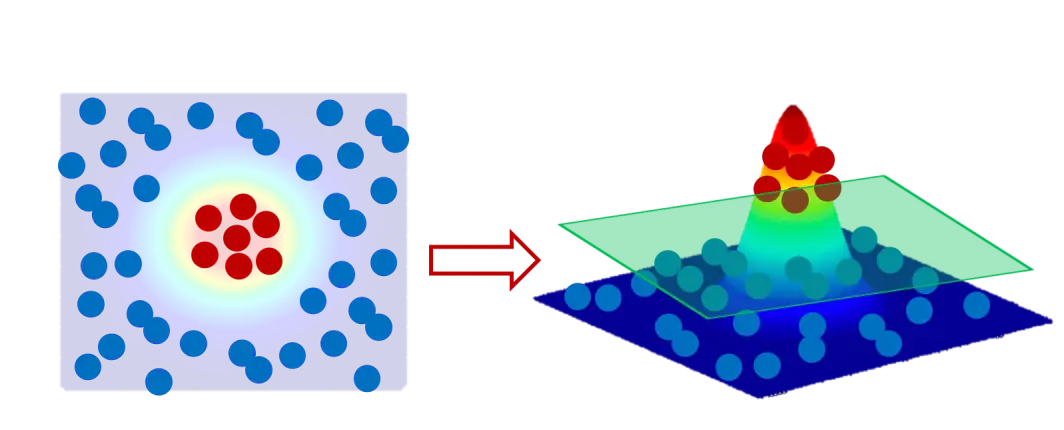
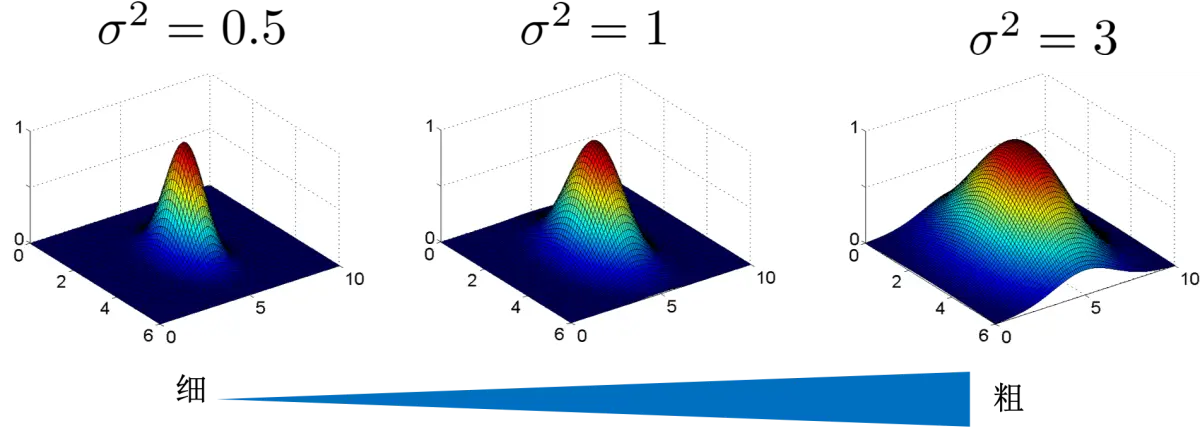
但是怎么提起来这些点呢?这个时候就需要“核”了。最常用的比如高斯函数作为核(radial basis function kernel,RBF kernal):
什么是核
简单来说,使用核将数据转换为另一个维度,该维度使数据类之间具有更明确的划分边界。其实就是将在 $n-1$ 空间中不能线性分离的数据在 $n$ 维空间中线性分离。
关于“核”的作用,还可以看看《三体 3》 第一部第一节“魔法师之死”。
使用核函数(比如这里的高斯函数)将原始二维数据变换到三维空间,就能将原始数据中想要提起来的部分提起来,从而使用平面(准确地说是超平面)将数据线性分类。
上图的 $\sigma^2$ 代表高斯函数的方差,方差越大,高斯函数越胖。可以想象,高斯函数越瘦,提起来的点越少,但是能更精确的控制提起来那些点。高斯函数越胖,提起来的点越多,但是却只能更模糊地确定提起来那些点。
前面叙述的没有使用核技巧的支持向量机,也经常叫做线性核。
模型调参
支持向量机的模型出现了一些超参数需要我们自己调节。为了调试出更好的模型,我们需要更深入地理解支持向量机的原理。
线性核
首先从最简单的线性核的线性分类入手。
以二维平面为例,就是一条直线就能将数据分为两类。比如一个线性分类器为:
\[f(x) = wx + b\]判定边界为 $f(x)=0$,将两边数据可以很好地分类。将数据归一化,然后规定 $f(x) \geq 1$ 为一类,$f(x) \leq -1$ 为另一类。两条平行线$f(x) = 1$ 与 $f(x) = -1$ 之间的距离为支持向量机的边界宽度:
\[margin = \dfrac{2}{\|w\|}\]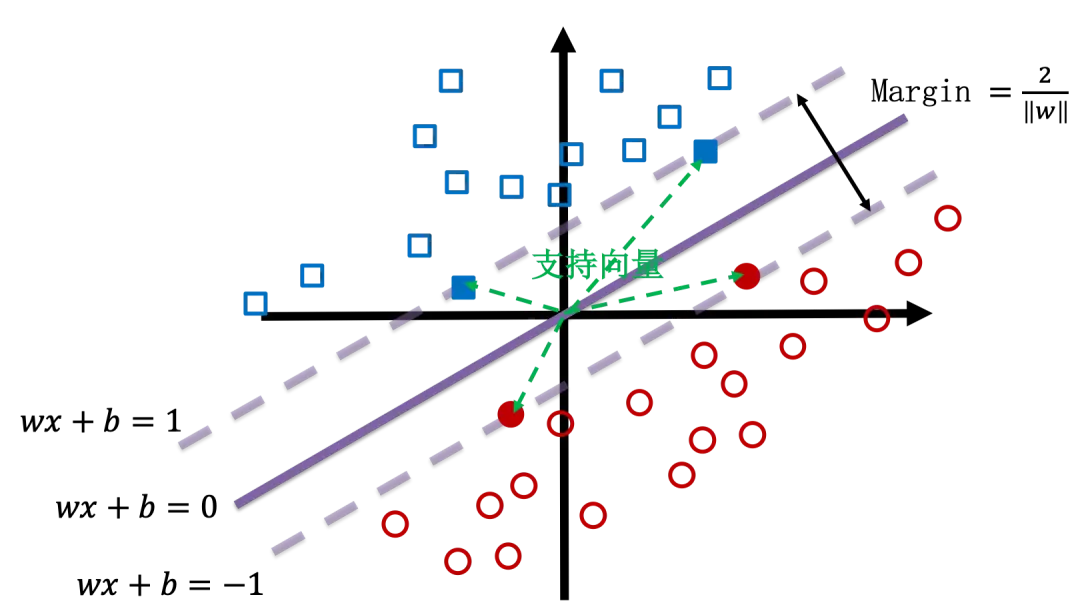
支持向量机想要让边界尽量宽,也就是要 $margin = \dfrac{2}{|w|}$ 尽量大,或者说是要 $|w|^2$ 尽量小。但是也要求不要有什么错误发生,也就是分类尽量要对,即 Hinge Loss 尽量小。结合这两个要求,支持向量机正则化的损失函数可以写作:
\[\|w\|^2 + C (Hinge \ Loss)\]其中,$C$ 是一个正则化参数且 $C \geq 0$。支持向量机就是要最小化这个损失函数。其中 $|w|^2$ 奖励宽的边界,越宽越好。而 $C (Hinge \ Loss)$ 惩罚错误,错误越少越好。但是可以想象,边界更宽,必然带来错误的增多,这个矛盾怎么解决呢?我们一般通过设置 $C$ 来权衡利弊:
- $C$ 小的话,损失函数受到 Hinge Loss 的影响小,也就是对错误的惩罚小,或者说对错误的容忍大,模型更严厉,从而使边界可以更宽。$C$ 如果等于 0, 那 Hinge Loss 就完全没有影响了,对错误无惩罚。
- $C$ 大的话,损失函数受到 Hinge Loss 的影响大,也就是对错误的惩罚大,或者说对错误的容忍小,模型不那么严厉,从而要求边界更窄。$C$ 如果等于 $+\infty$, 那只要 $C \neq 0$ 损失函数就无穷大,对错误零容忍。
$C$ 可以理解为决定了支持向量机模型有多严厉,也就是它对错误有多么不能忍。
结果上来看,可能会看到下图的情况:
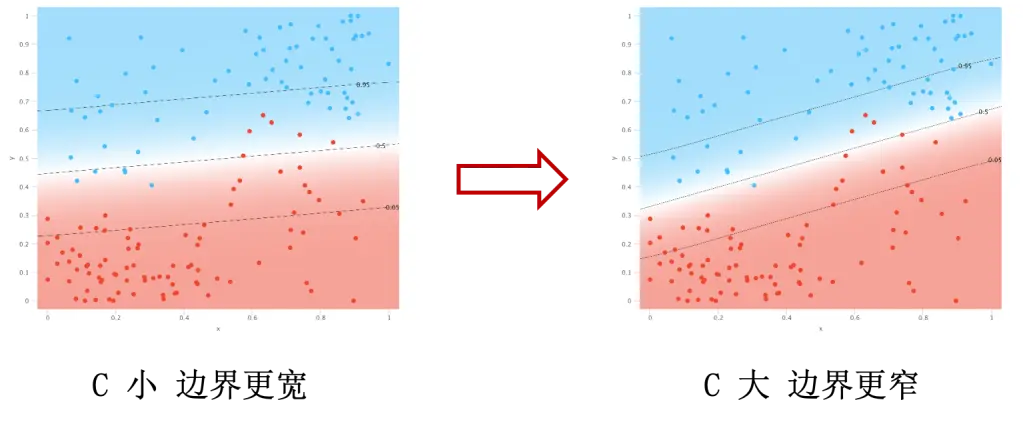
从图上可以看出,蓝色点主要分布在右上角,红色点主要分布在左下角。$C$ 大导致分类错误较少,但是却让蓝色和红色点的主体部分更接近边界。一般来说,新的数据更可能会出现在点密度大的地方,如果 $C$ 过大,更容易导致新的数据点判断出错。但是 $C$ 太小也会导致现有数据分类错误过多的问题,所以需要我们找到一个合适的 $C$ 来保证模型工作在理想的状态。$C$ 可以理解为模型的严厉程度。
非线性核
模型的严厉程度
下面再看看在非线性情况下,也就是使用核技巧的时候,模型的严厉程度会有什么表现。
首先明确,不管有没有核,损失函数总体上都是如下是形式,也即是想让边界更宽而错误更少:
\[\|w\|^2 + C (Hinge \ Loss)\]下面仅仅以 RBF 为例说明。
$C$ 的作用和线性模型时候一样,结果上来看,可能会看到下图的情况:
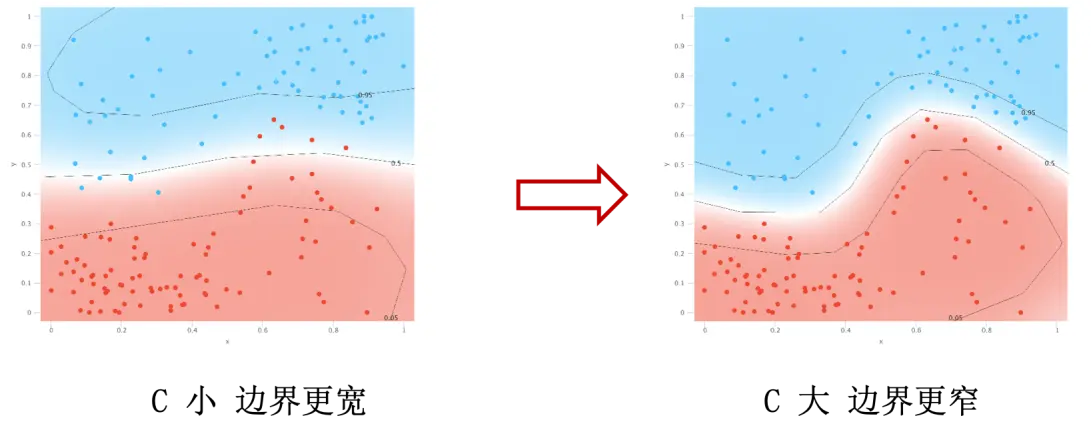
$C$ 大导致边界线弯弯曲曲的,容易产生过拟合。但是 $C$ 太小也会导致分类错误过多的问题,所以需要我们找到一个合适的 $C$ 来保证模型工作在理想的状态。
胆怯程度
再看看在使用核技巧的情况下,支持向量机的数据有多胆怯,也就是边界远处的点会不会“不敢”参与到分类。
结合高斯函数的图形,我们可以发现方差越大,高斯函数越胖,峰顶的点影响范围越大。方差越小,高斯函数越瘦,峰顶的点影响范围越小。如果以山脚为判定边界,那就是说方差越大,离判定边界越远的点影响越大。这个影响范围,我们通过一个参数 $gamma$ 或者 $\gamma$ 来表示。对于高斯函数来说,$\gamma$ 反比于其方差。我们可以通过设置 $\gamma$ 来权衡单个数据的影响范围:
- $\gamma$ 小的话,山峰更平坦,离判定边界远的点也有影响,会更加积极地扩大势力范围。这种情况下,就要综合考虑近的和远的点的影响,因为它们都想离得边界远一些,而近的点是否划分正确并不是考虑的首要因素。
- $\gamma$ 大的话,山峰更尖,只有离判定边界近的点有影响,远处的点不具备影响力,远处的点更加胆怯而不愿意参与到划分中。这种情况下,就要尽可能使边界附近的点划分正确,而不太考虑远处的点的影响,从而导致边界更加弯弯曲曲。
结果上来看,可能会看到下图类似的情况:
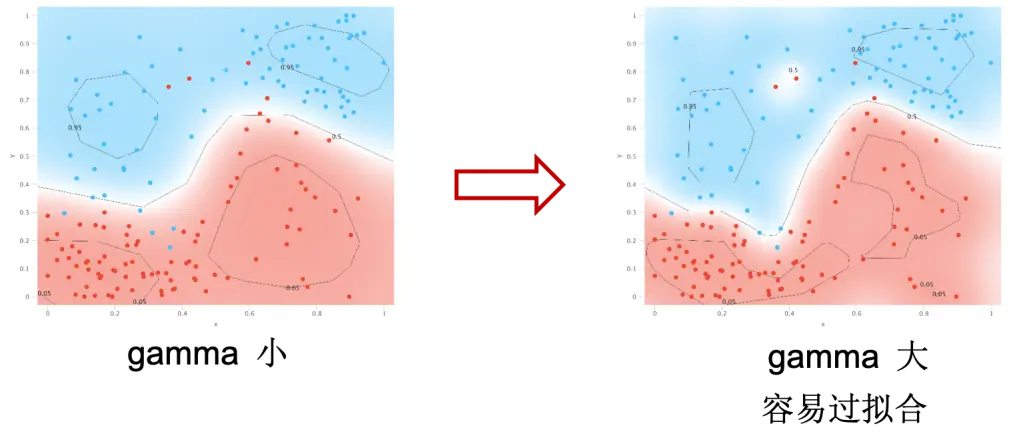
$\gamma$ 大导致边界线弯弯曲曲,容易产生过拟合。但是 $\gamma$ 太小也会导致分类错误过多的问题,所以需要我们找到一个合适的 $\gamma$ 来保证模型工作在理想的状态。$\gamma$ 可以理解为数据的胆怯程度。
$C$ 与 $\gamma$
从表现上看,二者小都会导致边界“更直”,大都会导致边界“弯曲”,但是其背后的原因是不同的。举个例子,想象每个数据都是一个人,模型是一种规矩,$C$ 是的规矩严厉程度, $\gamma$ 就是每个人有多胆怯,判定边界就是根据规矩是否犯错的准则。
- 如果规矩没有要求严厉执行,大家就不那么怕犯错误了,就会更自信的抬头挺胸一直往前走;如果规矩要求严厉执行,大家很怕犯错误了,大家就会小心翼翼地左探探右探探,脚印都要严格对在前面的人的脚印上,很难走出一条直线。
- 如果大家特别胆怯,除非逼得他们必须做决定,就不敢做太多决定,而那些被逼必须做决定的人就会死盯着规矩,带着大家小心翼翼地左探探右探探,脚印都要严格对在前面的人的脚印上,很难走出一条直线;如果大家没有很胆怯,就敢做更多决定,集体的决定往往更中庸而不偏激,就会走出一条更直的道路来。
反馈问题
文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈
点我反馈进入反馈页面不知道如何反馈, 请点击这里