决策树
决策树也称作分类树或回归树。叶子节点给出分类,内部节点代表某个特征,分支代表某个决策规则。构建决策树时通常采用自上而下的方法,在每一步选择一个最好的属性来分裂。”最好” 的定义是使得子节点中的训练集尽量的纯。不同的算法使用不同的指标来定义”最好”。
决策树的优点
与其他的数据挖掘算法相比,决策树有许多优点:
- 易于理解和解释。
- 数据不需要归一化等处理。
- 易于可视化。
以我们熟悉的泰坦尼克号生存问题为例,其决策树可能如下:
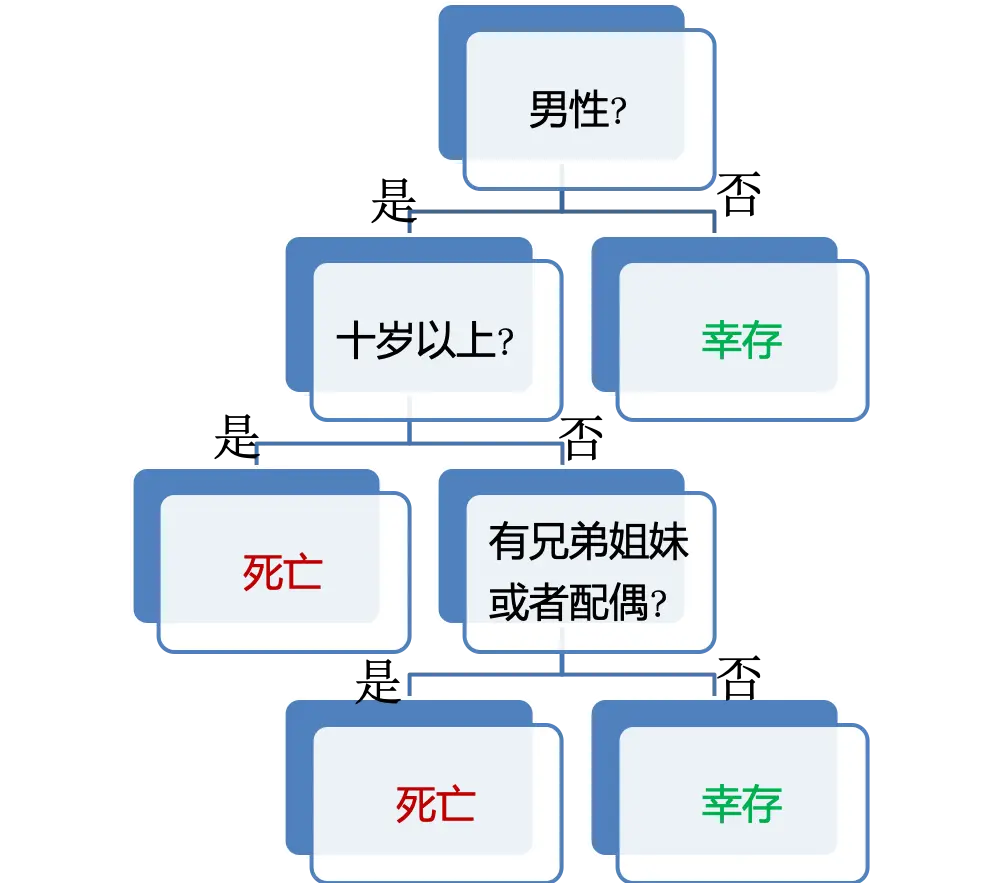
详细没有任何决策树知识的读者也能看出来这张图的意思吧。一图胜千言,这张图已经充分说明了以上三个优点了。
决策树的缺点
决策树缺点:
- 容易过拟合。
- 如果某些类别占据主导地位,则决策树学习器构建的决策树会有偏差。因此推荐做法是在数据集与决策树拟合之前先使数据集保持均衡。
防止过拟合
决策树算法关键问题之一是最终树的最佳大小到底是多大。
- 树太小可能无法捕获有关样本空间的重要结构信息。比如熟知的泰坦尼克号生存预测问题,最简单地我们可以认为只要是男人就是死亡,否则就是存活。这个树就只有两个树枝,不能更简单了,但是这个树没有使用更多的特征来做预测,很难有足够的准确性。这个情况是欠拟合。
- 树太大会考虑过多的细节,导致很难推广到新的样本,导致过拟合。
下面主要讨论过拟合问题及怎么解决这个问题。
问题解析
比如对如下数据做分类:
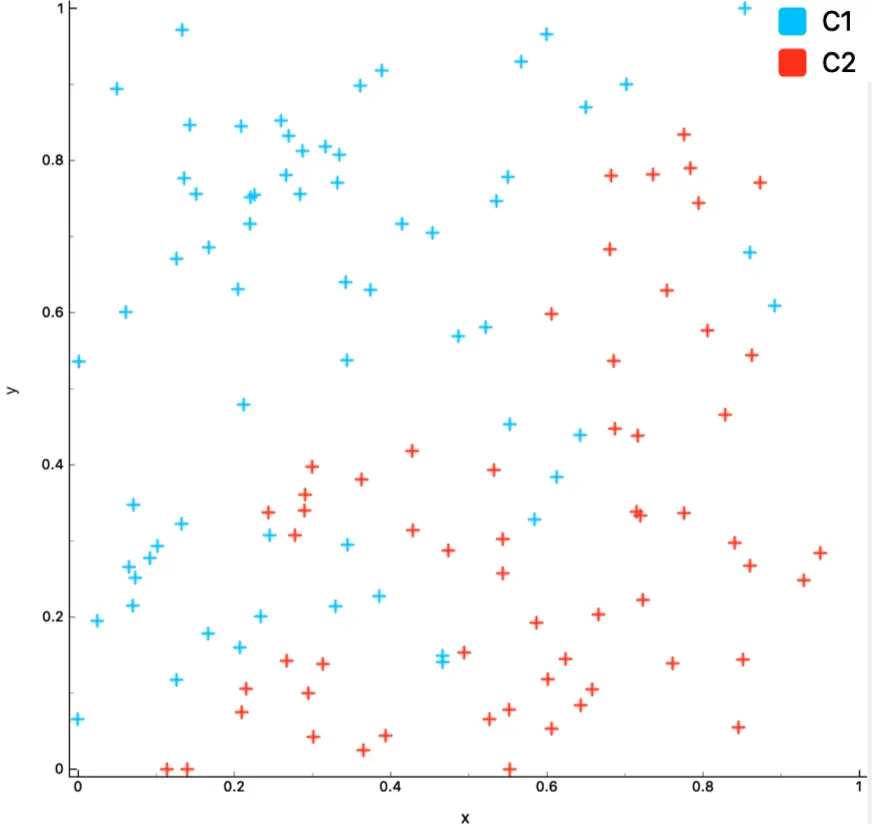
其分类树的一种可能构造如下:
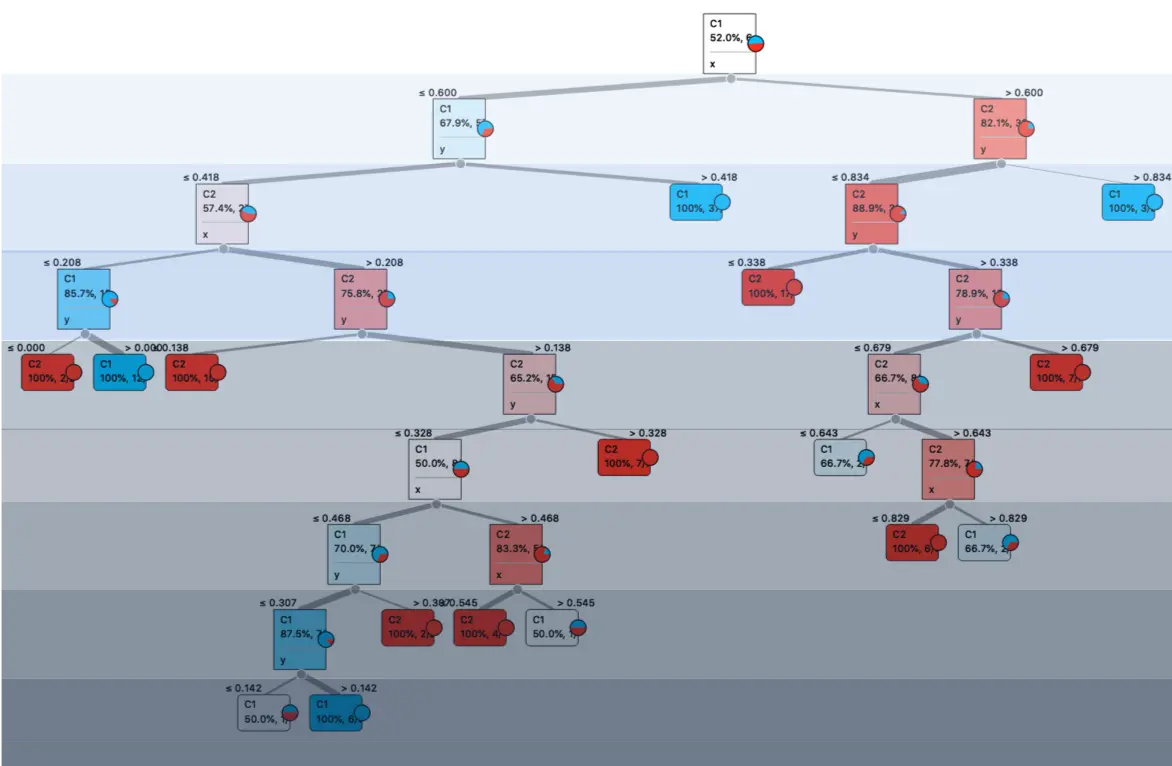
观察这棵树,问自己三个问题:
- 需要这么深的树吗?
- 随着节点深度增大,错误率下降的够快吗?
- 某些节点的样本数目会不会太少了?
这三个问题就带给我们两种解决办法:
- 出现问题之前预防问题的发生
- 出现问题之后解决掉问题
这两种解决办法为:
- 提前结束
- 剪枝
奥卡姆剃刀
这两个方法共同特点是减少树的大小,哲学基础都可以看作是奥卡姆剃刀。它是由14世纪英格兰的逻辑学家、圣方济各会修士奥卡姆的威廉(William of Occam,约1285年至1349年)提出。这个原理称为“如无必要,勿增实体”,即“简单有效原理”。
提前结束
首先来看看提前结束。顾名思义,就是不要把树构建到最后一层那么深,而是提前就结束构建。提前结束有三种方法:
- 限制树的深度
- 根据错误率决定是否结束
- 节点中的数据过少
限制树的深度
随着树的深度变大,过拟合的可能性就会大大提高。
为了降低过拟合的风险,我们可以选择在合适的深度位置停止树的生长,最好的位置当然就是选在其他数据的损失函数最小的位置了。
错误率阈值
限制树的深度可能有一个问题,有的分支可能深一些更好,有的分支可能浅一些好,而深度限制却简单粗暴地只给了一个深度限制。所以另外一个方法就是根据分类的错误率决定是否结束。如果错误率降低的速度小于阈值那就停止。
样本数阈值
另一个极其重要的提前结束的方法是样本数阈值。数据分类到一定时候,数据量已经很少,不具备足够的代表性了,这个时候就结束树的生长。这个方法建议强制应用,而且也是很多机器学习工具默认使用的。
提前结束的优缺点
- 优点:不需要完全展开所有数据,速度快
- 缺点:可能结束太早,导致欠拟合(过拟合的反面)
你可能会想,怎么可能结束太早呢?从图上可以很清楚看出来啊?但是前面展示的图太理想了,真是的情况可能比下图还糟糕:
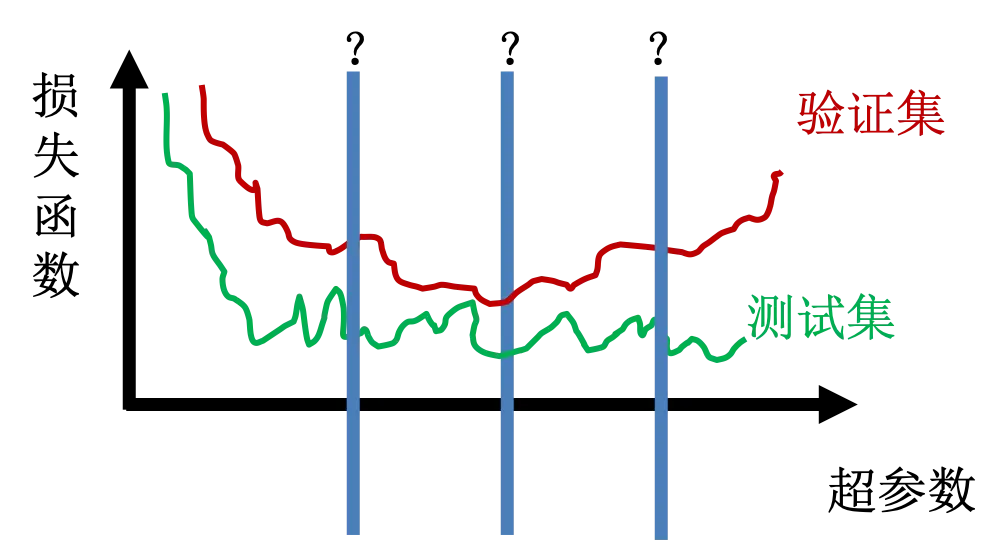
为了防止过于提前结束,我们可以用剪枝解决欠拟合问题。实际上,提前结束也叫预剪枝这里说的剪枝也叫后剪枝。
剪枝
剪枝(Pruning)顾名思义就是把细枝末节剪掉,防止模型陷入细节。其最基本的方法就是先将整个树长出来,然后根据错误率修剪掉不需要的枝叶。
剪枝删除树的细枝末节减小决策树的大小,降低了最终分类器的复杂性,因此通过减少过拟合来提高预测精度。
这里介绍一种后剪枝技术。如果父节点错误率比子节点少就剪掉子节点,也就是子节点不能降低错误率那就不要子节点了。如图:
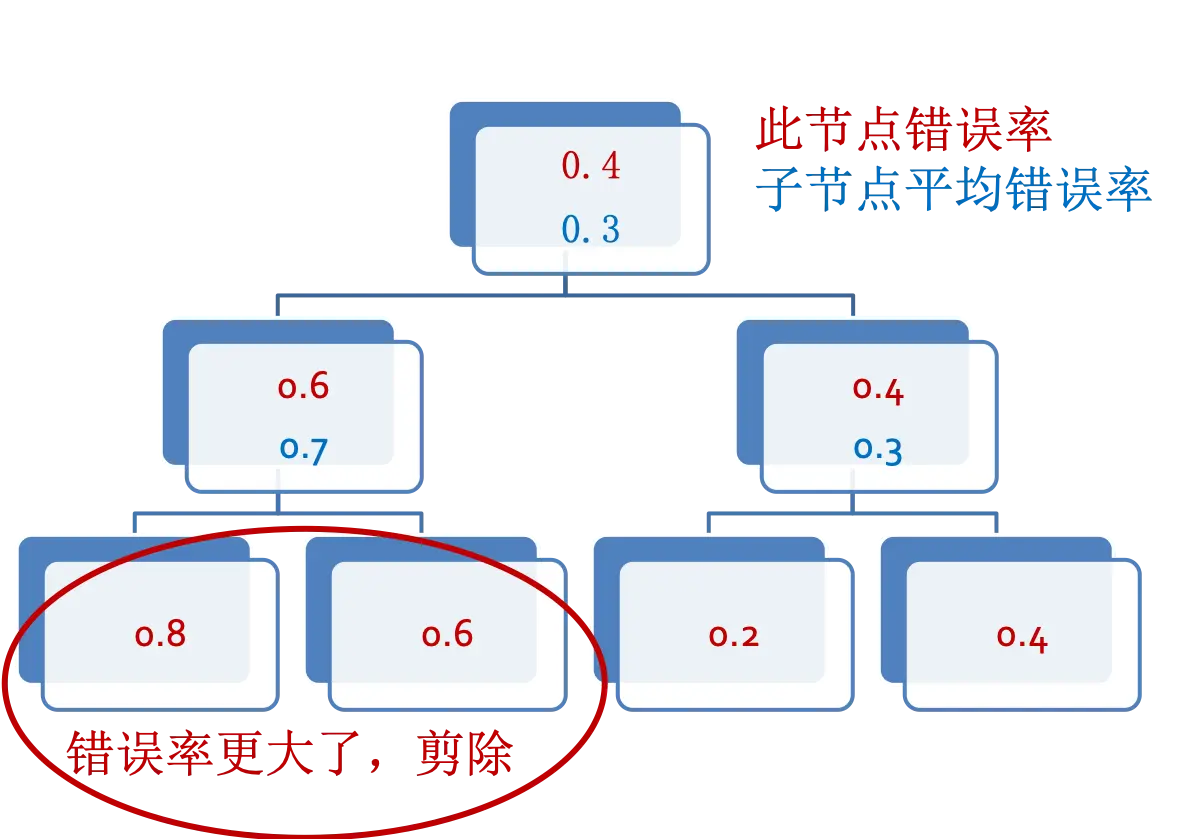
组合算法
模型简单了不准,复杂了也不准,怎么办?模型可以做到三个臭皮匠赛过诸葛亮可能吗?弱分类器可以组合成强分类器吗?
组合算法(Ensemble)使用若干个弱分类器组成一个强分类器,试图达到三个臭皮匠赛过诸葛亮的效果。它可以提高模型的准确率和健壮性,主要有几种方法:
- 袋装(Bagging, Bootstrap AGGregatING)
- 堆叠(Stacking)
- 随机森林(Ramdom Forest)
- 提升(Boosting)
自助抽样
在理解上述三种算法前,我们先了解一下什么是自助抽样(Boostrap)。自助抽样就是随机有放回抽样。比如一个袋子里面放了不同颜色的球,我从里面随机拿出来一个球记录一下颜色又放回去,接着再从袋子里随机拿一个出来记录再放回去,如此反复。
袋装
投票方法是袋装常用的一种方法。从训练集中自助抽样出 n 个样本集,建立 n 个决策树模型,然后这几个模型投票决定结果。比如说泰坦尼克号模型,假设我进行了三次自助抽样,对应地使用了三个分类器,分别对一个数据给出“生”,“生”,“死”的预测。根据少数服从多数的原则,最终分类结果为“生”。由于是投票决定,放了防止平局,最好采取奇数次数目的抽样。
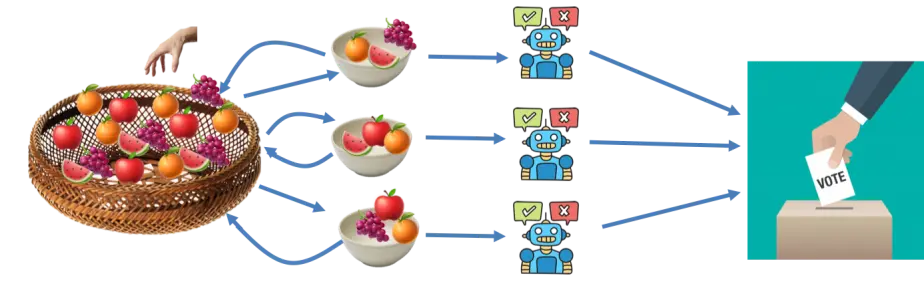
通过几个模型的综合作用,可以在降低偏离的情况下同时降低方差,也就是准确性和健壮性都提高了。假设每一个结果都给出了一个可能的取值及其概率,最后袋装的结果就是将这些结果综合考虑,判断到底哪个取值的概率更大
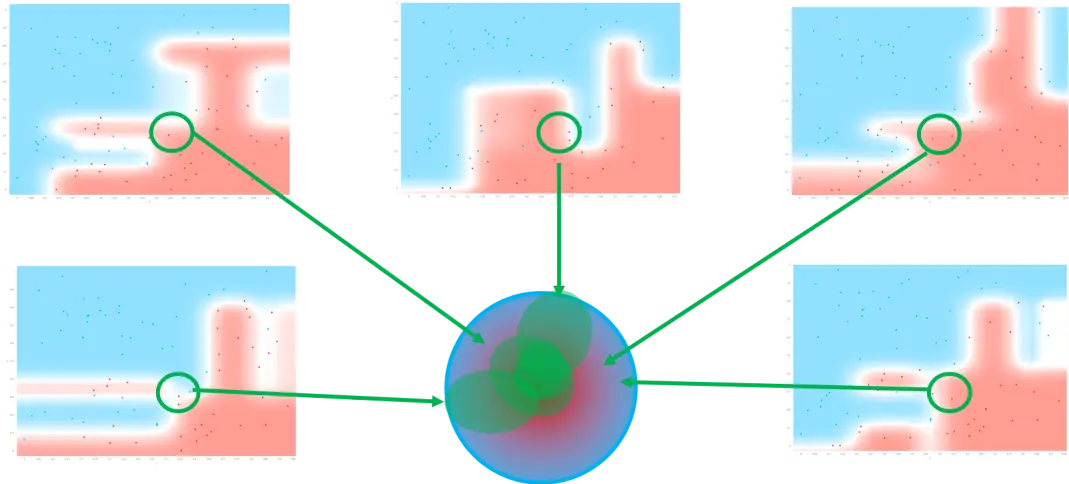
堆叠
堆叠类似袋装,最大的不同就是投票阶段。在堆叠中,不是袋装简单的“谁多听谁的”,而是将各个模型的预测结果作为输入,通入到另一个“集成者”(就是任意一个可用的机器学习模型,比如逻辑回归模型),让它判断最后结果到底是什么
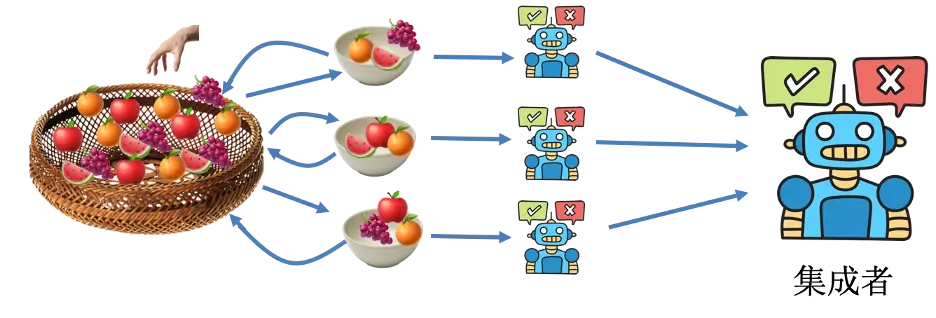
随机森林
类似袋装进行自助抽样,而且对特征也进行抽样,每次抽 m 个特征( m 一般为所有特征数的平方根)。对特征抽样是为了防止特征之间的相关性对模型的影响。
提升Boosting
与装袋类似,基本思想方法都是把多个弱分类器集成成强分类器。不过与装袋不同,装袋的每一步都是独立抽样的,提升中每一次迭代则是基于前一次的数据进行修正,提高前一次模型中分错样本在下次抽中的概率。打个比方,就像一个学生将每次练习和考试的错题集成成了一个错题本,然后针对这个错题本学习。错题本做了一次之后,可能再次根据错误总结出一个新的错题本,接着再用新的错题本学习,不断提高成绩
Adaboosting
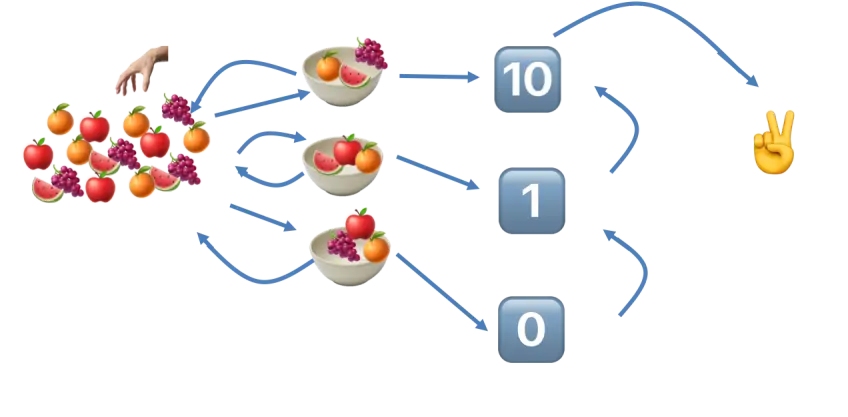
Adaboosting(Adaptive Boosting)即自适应提升,其自适应在于:前一个分类器分错的样本会被用来训练下一个分类器。我们通过图解了解一下这个过程。假设对下图的两种颜色的点分类:

这个时候每一个数据的权重都一样,模型 f1 简单地如下图做了分类:
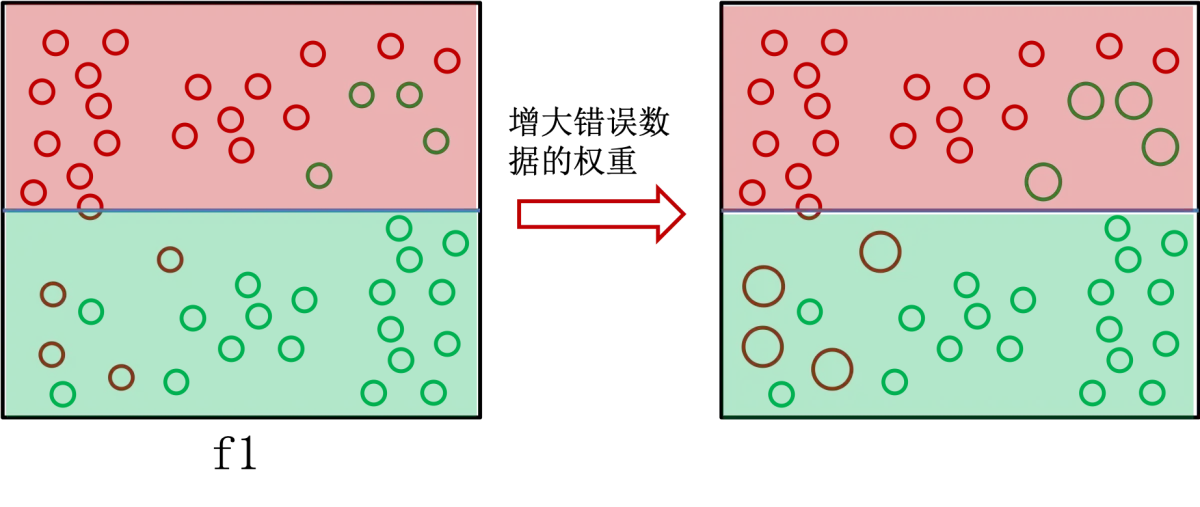
可以发现,有大量的划分错误,这个时候算法增大错误数据的权重,图中显示就是增大了点的大小。由于模型 f1 错误的数据权重增大了,所以模型 f2 会更注重将 f1 分错的点分对,即如下分类:
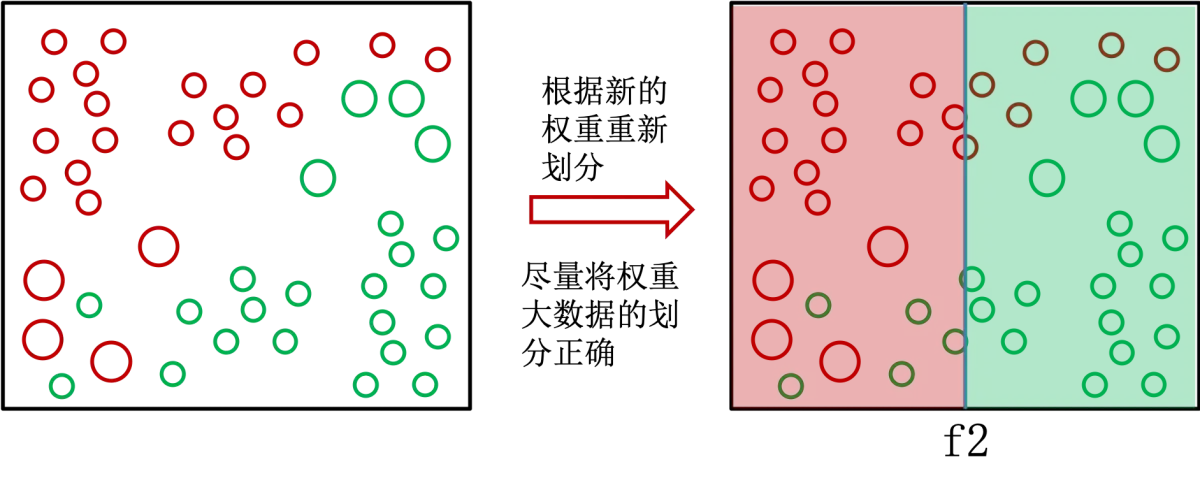
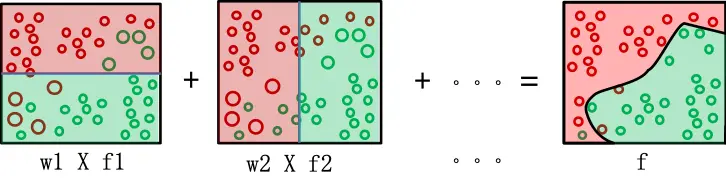
根据模型的错误率给模型赋予权重,错误率低权重就高,错误率高权重就低,也就是算法更看重分类效果好的模型的预测结果。然后将模型的预测结果加权相加,就是最后 Adaboosting 的结果。

通过增多弱分类器的数目,就可以提高最终模型的准确率了。
反馈问题
文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈
点我反馈进入反馈页面不知道如何反馈, 请点击这里