梯度与梯度下降

在模型的训练过程中，会涉及到大量的参数设置问题，如何更快更好地设置这些参数，直接关系到最终模型的好坏。理解梯度下降算法，可以帮助我们调试出更好的模型。

前面介绍过损失函数，用来估量模型的预测值与真实值的不一致程度。

如何使损失函数最小化呢？我们使用梯度下降算法计算损失函数的最小值

但是梯度是什么呢?

梯度

以等高线为例说明。在某一点，垂直于等高线走的线就是梯度线。而梯度本身是一个标量。

梯度下降

怎样找到最低的那个点呢？梯度下降算法简单地说就是沿着梯度走下来。

具体怎么知道应该朝那个方向走呢？$下一个位置 = 当前位置 - 学习率 \times 梯度$，这里的学习率是一个正数，一个超参数，也就是一个靠经验设置的一个值。

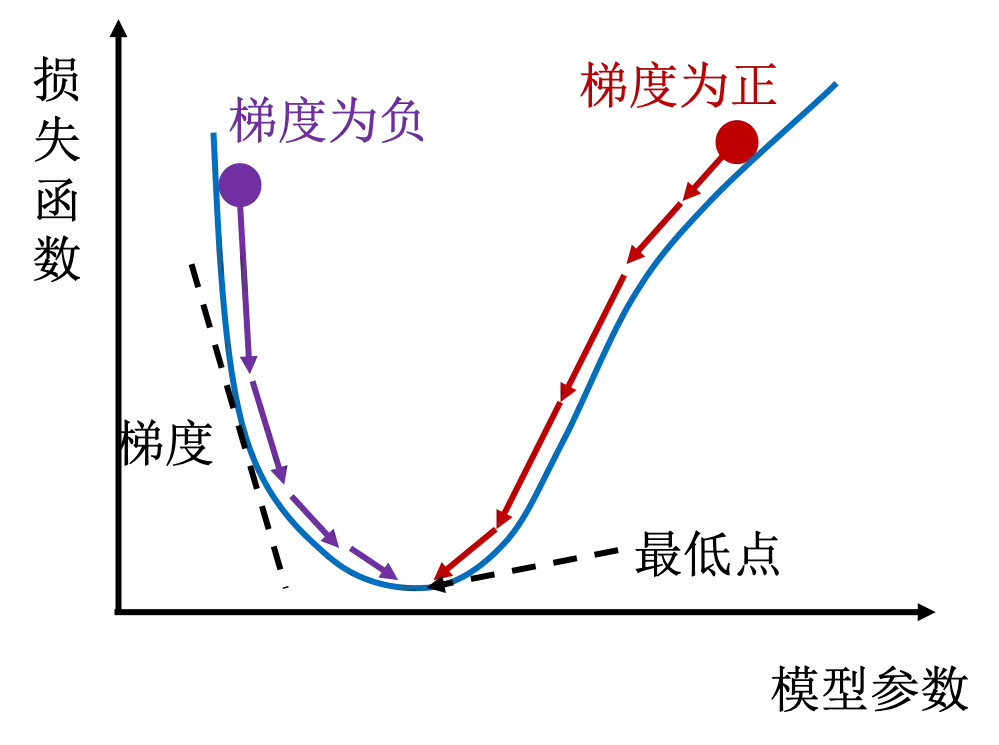
如上图所示的曲线，左侧梯度为负，右侧梯度为正。当初始位置在右侧时，下一个位置会比当前位置低。循环计算下一个位置，慢慢就会找到最低点。每一个循环叫做一个周期（Epoch）

学习率（Learing Rate）

使用梯度下降算法有一个学习率的问题，太大或者太小都不好。观察梯度下降算法示意图，想想为什么。

结合下图看看学习率大小的问题：

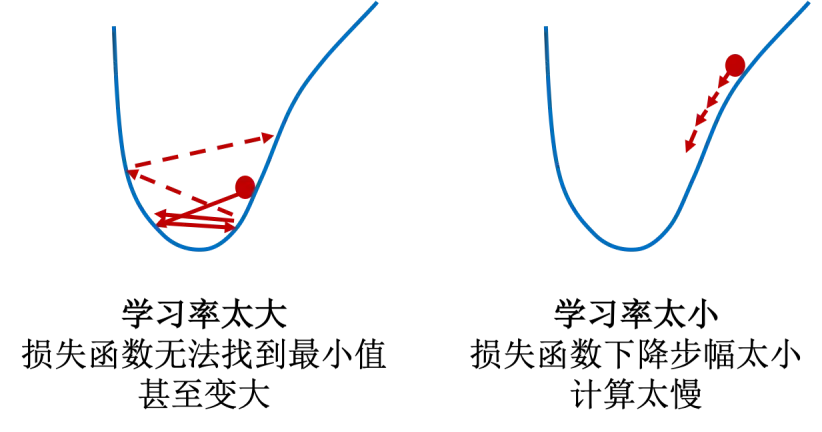
如果学习率太大，会产生每一步迈得太大的问题，将梯度直接从正数变为负数，导致损失函数梯度正负之间来回震荡而不能下降。反之，如果学习率太小，每一步都谨小慎微，虽然损失函梯度绝对值一直降低，但是步子太小，效率太低。所以，如何设置学习率，是一个考验机器学习工程师能力和经验的艺术。

结束标准

怎么样才知道什么时候可以使梯度下降算法循环结束呢？我们有两个标准，满足一个即可截止：

• 损失函数小于阈值（$\epsilon$）
• 已经运行了设置的最大周期数

梯度下降算法是否正常工作

想要知道梯度下降算法是否正常工作怎么办？我们可以画出画出损失函数每个周期的变化。

正常情况下，损失函数应该随着周期数持续下降，最后稳定在某个值的附近，如下图所示。

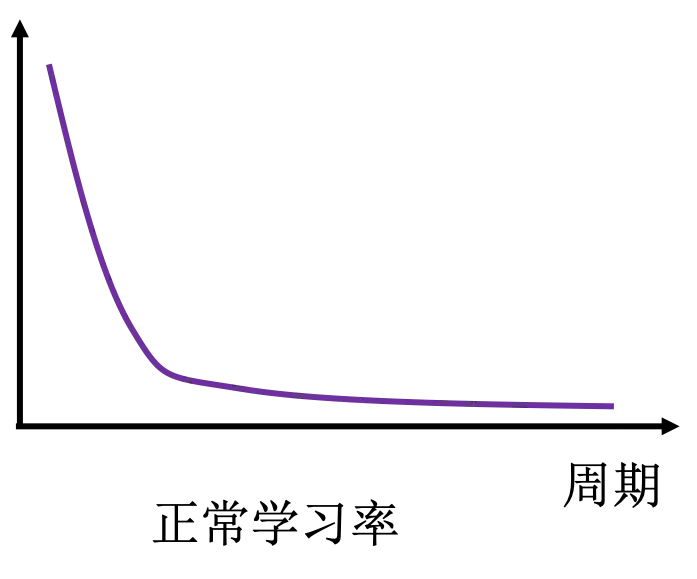
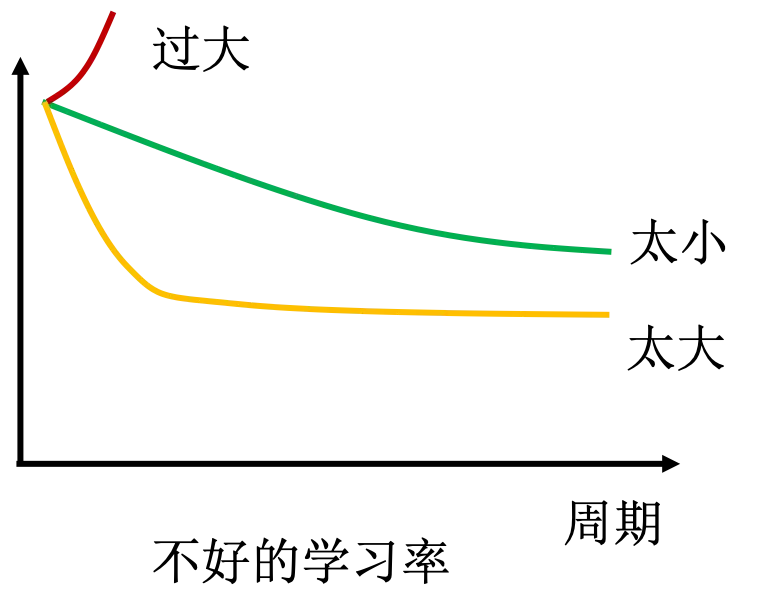
但是如果学习率太小，将会发现损失函数一直下降，但是不能稳定，这就是因为上面说的不在太小，一直达不到最低点附近。但是如果学习率太大，将会发现损失函数很快下降到某个比较大的值附近，便不再变化，说明损失函数的梯度值发生了震荡。假设发现损失函数不降反升，那就说明学习率设置的过于巨大了，导致梯度更新的每一步都上升而不是下降。

梯度下降算法的种类

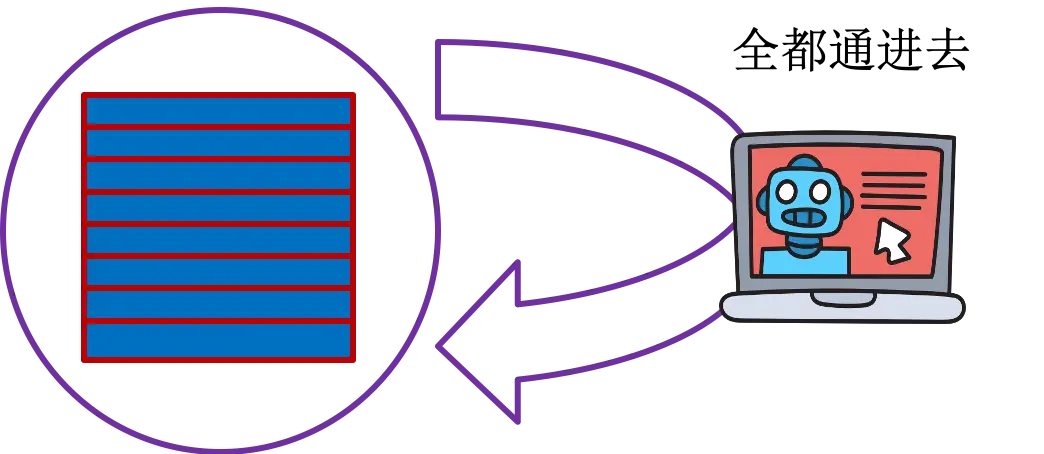
Batch Gradient Descent

这种方法中，所有样本一起参与计算梯度，所有参数同时更新，计算效率高，内存需求大，有可能不能到达最优解

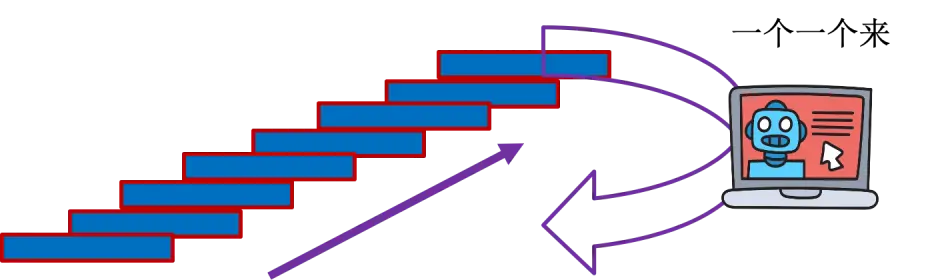
Stochastic Gradient Descent（SGD）

这种方法中，样本一个一个地参与计算梯度，计算资源消耗大，计算不是很稳定

Mini-batch Gradient Descent

这个方法结合上面两个算法，样本分成若干份，一份一份参与梯度计算，从而达到稳定与快速相结合

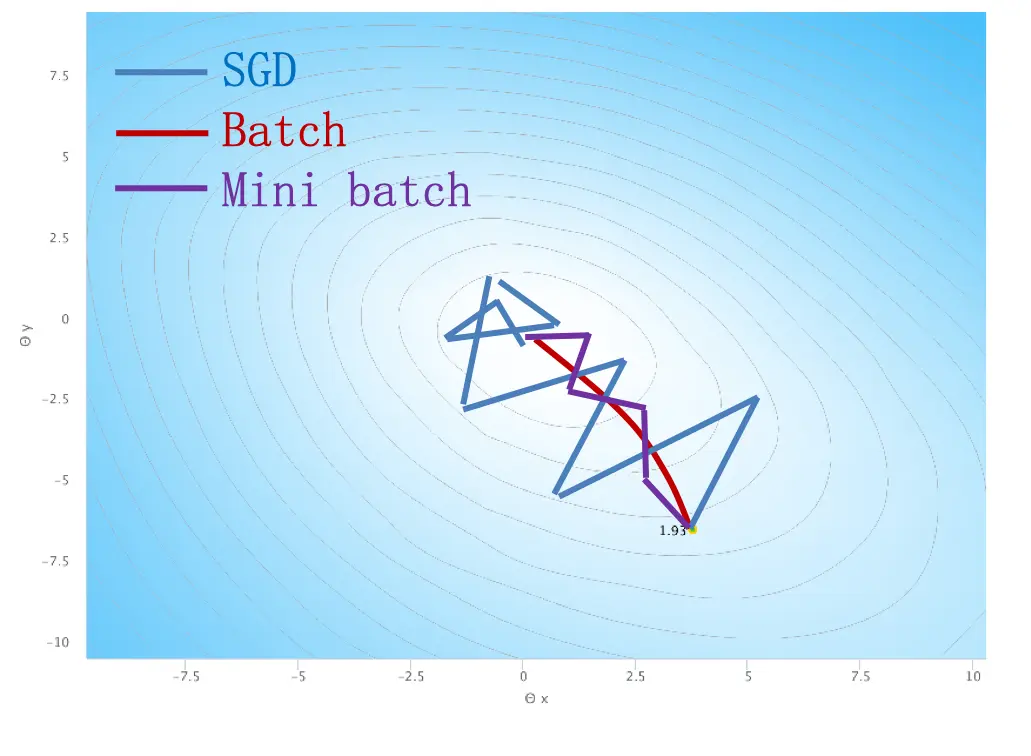
综合比较

如果比较这几种算法，可以发现他们的运行路径十分不同。 Batch Gradient Descent的所有参数同时参与运算，所以总体来说梯度朝着固定的方向变换，曲线平滑。而 SGD 算法因为样本一个一个地参与计算梯度，所以不能保证每次运算都能够减小梯度，从而导致曲线乱撞。Mini-batch Gradient Descent 则综合两种方法，所以虽然也比较抖动，但是朝着一个方向前进的趋势更加明显。

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里