过拟合与欠拟合

过拟合将会是机器学习的极大障碍，它是模型完美地或者很好地拟合了数据集的某一部分，但是此模型很可能并不能用来预测数据集的其他部分。

概述

如果学生只是背会了作业答案，而考试如果只考作业题目，考试成绩肯定很好。但是考试如果是新的题目呢？那考试分数将会惨不忍睹。这就是一种过拟合，即考试范围出了作业范围就无能为力了。我们在学习科学知识的时候都强调要理解原理，而不是背会某个题，就是为了让自己能够有更好的“泛化能力，做到举一反三。

比如下图所示数据，其实用一条直线拟合就挺好，但是为了完美拟合，使用了相当复杂的曲线连接，很难保证模型能够覆盖之后出现在直线附近的点，尤其是超出目前坐标范围的点，这就是一种典型的过拟合。

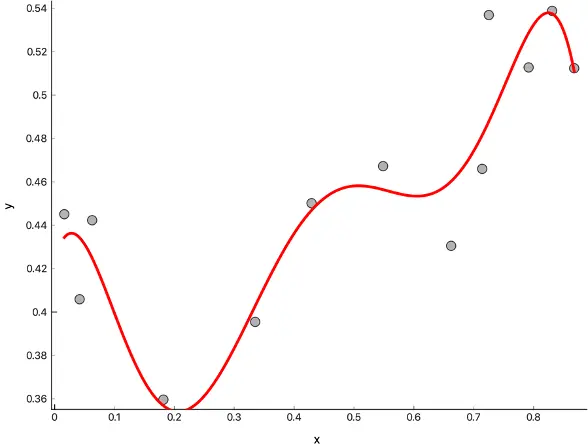
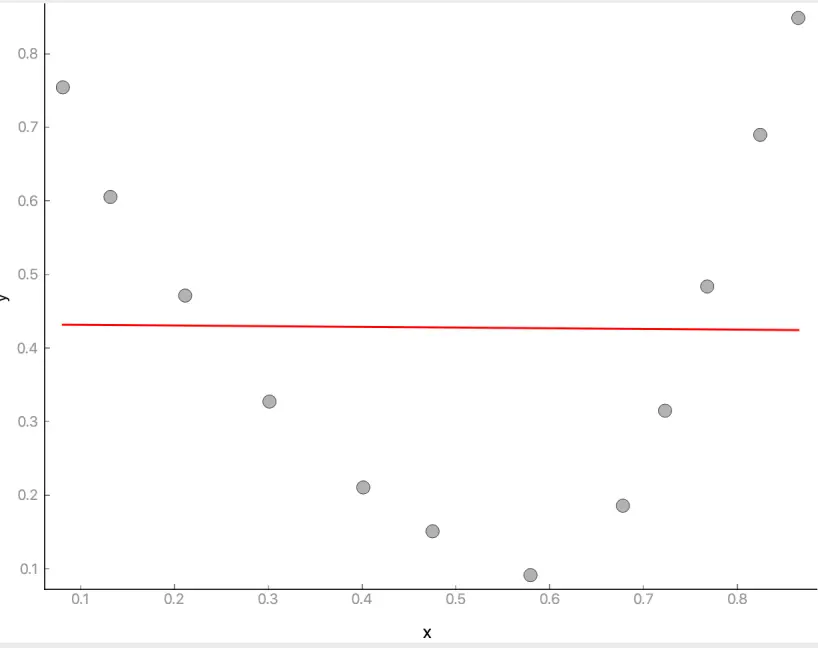
欠拟合正好相反, 本来应该用更复杂的曲线拟合, 但是却只用了简单的曲线, 例如下图:

损失函数看过拟合

随着树的深度变大，过拟合的可能性就会大大提高。我们将数据分为训练数据和其他数据，观察二者损失函数的变化，可见如下图损失函数变化。

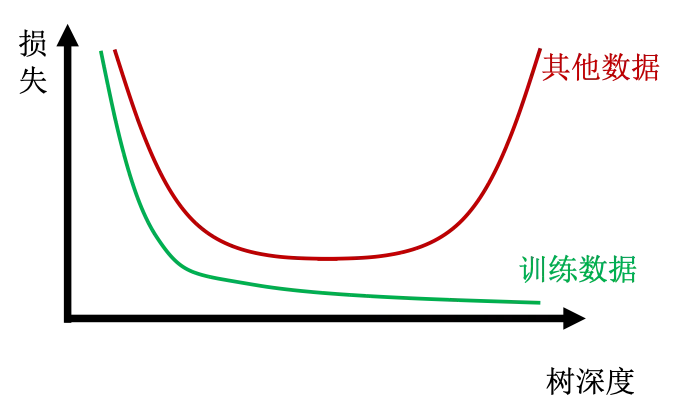
可以发现，训练数据的损失函数会随着树的深度增加而逐渐降低，但是其他数据很可能会经历一个先降低又升高的过程。这个升高的过程就说明模型出现了过拟合的问题。

判定边界看过拟合

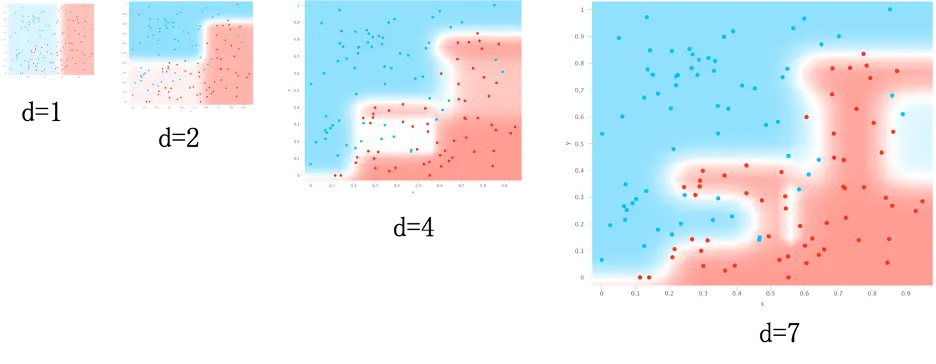
我们可以从判定边界角度看看这种过拟合的风险。如下图决策树模型为例, 可以发现，随着深度的增加，边界越来越复杂。当 𝑑=1 时，仅仅是一条线。但是当 𝑑=7 时，情况已经相当复杂，这个时候很可能已经过拟合了。

偏差大与方差大

前面介绍过，过拟合就是模型完美地或者很好地拟合了数据集的某一部分，但是此模型很可能并不能用来预测数据集的其他部分。欠拟合正好反过来，模型拟合程度不高，数据距离拟合曲线较远，不能够很好地拟合数据。

欠拟合也叫高偏差

为什么欠拟合又有了新名字呢?

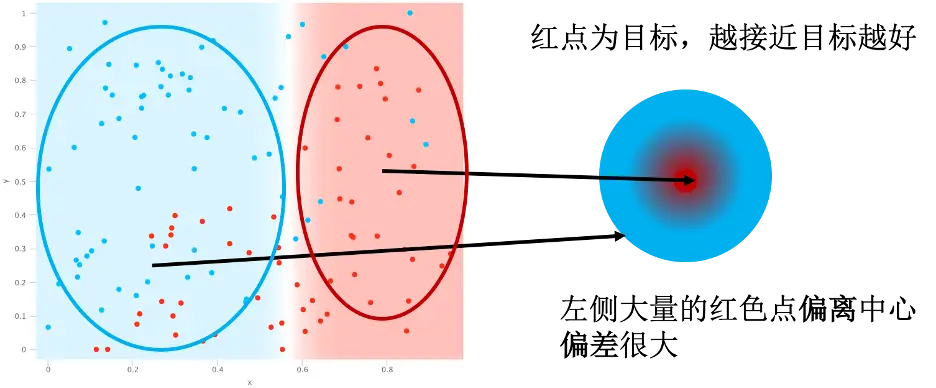
如图所示，左侧是任务数据图，右侧是其结果映射。假设我的任务是将左图的红点和蓝点分开，以正确判断红点为目标，模型能让左图数据中的红点映射到右侧靶心是最好的。左图红色和蓝色区域分界的白线就是判定边界。可以发现，判定边界右侧的所有点都映射在了靶心，而左侧所有点都远离了靶心。但是在判定边界两边都有大量误判的点，对于我们关心的红点来说，左侧大量的红点偏离中心，导致模型比较高的偏差。这个例子中，实际数据和拟合结果偏差很大，所以欠拟合也叫高偏差（high bias）。

同时可以注意到，这个例子中左图的点在相当大的范围内变化，都不会改变它在右边结果图中的映射位置，这说明模型对数据变化不敏感，比较健壮(robust)。

过拟合也叫高方差

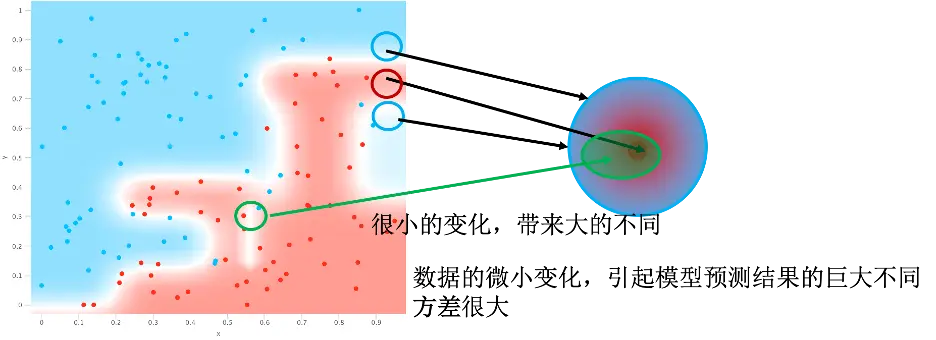
目标和上面一样，从下图我们可以看到，判定边界变得十分复杂。对应在右侧图上来看，左侧绿色圆圈内的点可能会对应到右侧映射区域的很大范围，结果导致数据的微小变化，引起模型预测结果巨大的不同，模型不够健壮。这说明数据的方差很大。所以过拟合也叫高方差。

欠拟合，过拟合与模型复杂度

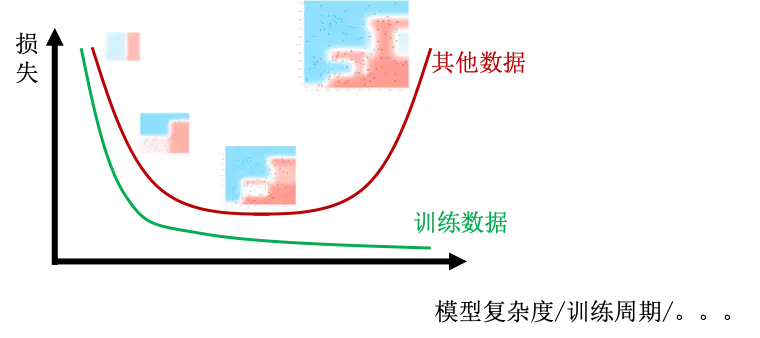
随着模型参数的增大，模型的增大，模型变得越来越复杂，模型也会慢慢得由欠拟合变为合适，进一步变为过拟合。如下图所示，模型简单的时候，各类数据的损失值都比较大，随着模型变大变复杂，各类数据的损失值都会下降。但是一旦模型过于复杂，虽然训练数据的损失值还会下降，但是其他数据的损失值却会上升。

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里