深入决策树
找到将数据最好地分类的特征,使用这个特征为根,使用某个规则分类数据,被分类的数据重复这个过程构建子树,直到完成构建。这句话隐藏着两个关键的问题:
- 什么是最好?
- 什么时候完成构建?
关于”什么时候完成构建?“已经在前面解决了,但是“最好”是什么呢?这步分我们就解决这个问题。
最好的衡量标准有很多,比较常见的有信息熵和基尼不纯度。他们分别使用于 ID3 算法和 CART 算法。
ID3 算法
ID3 (Iterative Dichotomiser 3)算法以信息论为基础,信息熵(Entropy ) 和 信息增益(Information gain)为衡量标准来回答什么是最好的问题。
CART 算法
CART (Classification and Regression Trees)算法是一种二分类递归算法,每一步只判断“是”或“否”,使用基尼不纯度来为衡量标准来回答什么是最好的问题。
待学习了下面部分熟悉了什么是“最好”之后,我们再研究下什么时候完成构建,也就是结束标准是什么。
ID3 算法决定什么是最好
首先我们来理解 ID3 算法要做什么。因为 ID3以信息熵(Entropy ) 和 信息增益(Information gain)为衡量标准,我们首先看看这里个概念。
熵
熵最初是一个热力学概念,用来系统混乱的程度。比如有三种形式存在的鸡蛋,我的问题是让你数一数一共多少个鸡蛋,你更愿意数哪个图呢?

不出意外的话,大多数人应该会选择数第一张图的鸡蛋,因为这张图最不“混乱”。
信息熵
信息论中,又叫做信息熵,是接收的每条消息中包含的信息的平均量。如果把上图看成三条信息的话,相信对于有多少鸡蛋这个问题,第一张图的信息量最足。
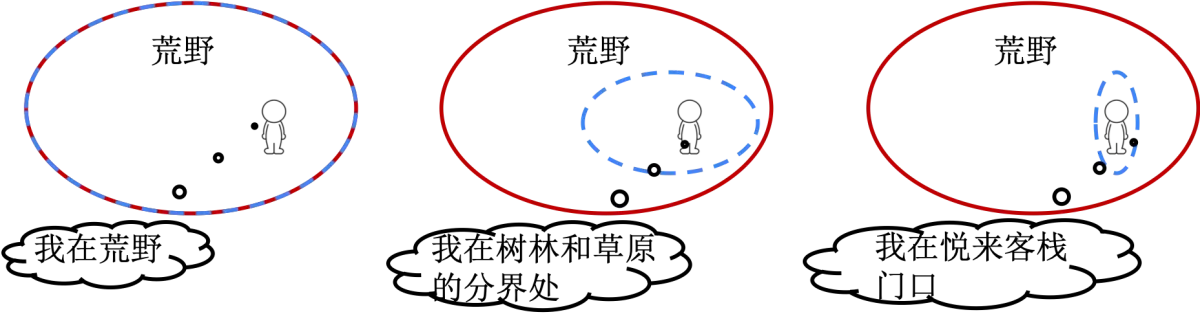
再举一个例子深入理解下信息熵,并了解其计算方法。假设你在荒野迷路了,但是手机又不能上网,唯一的方法就是打电话求助,但是你只能说一句话,你的位置如图,你准备说哪句话呢?
- 我在荒野
- 我在树林和草原的分界处
- 我在悦来客栈门口

假设你在搜寻的人眼中是在四处游荡的,也就是你在别人眼中出现在荒野任何地方的概率都是相等的。
- “我在荒野”这句话人人都知道,因为你100%是在荒野,显然这句话没有任何信息量。
- “我在树林和草原的分界处”这句话对信息的提升很有帮助,那么大的荒野,你能在这里的概率不高。这就是在一个平面上选了一条线,至少我知道要找的点在这条线上了。
- “我在悦来客栈门口”这句话就是告诉别人你的坐标了,那直接过去找你就行了。同时注意,你在这里出现的概率太小了,这句话的信息量太大了。
从这个例子中,你应该已经发现了,信息量越大,事件发生的概率越小。为了让信息量具有可加性,定义一个事件 $X$ 的信息量为概率倒数的对数:
\[I(X) = \log(\dfrac{1}{P(X)}) = -\log(P(X))\]在一个系统中,有着大量的事件,这些事件的信息量的期望(平均值)就是这个系统的熵
\[H(X) = E[I(X)] =\sum _{i=1}^{n}{\mathrm {P} (x_{i})\log_{b}\dfrac {1}{\mathrm {P} (x_{i})}} \\\]在这里 $n$ 代表事件有多少种可能性,$b$ 是对数所使用的底,通常是 2,自然常数 $e$,或是 10。当 $b = 2$(ID3 算法中的情况),熵的单位是比特(bit);当 $b = e$,熵的单位是奈特(nat);而当 $b = 10$,熵的单位是哈特(Hart)。
如果把每条消息看做一个系统,消息中每个比特看做是一个事件,信息熵就是接收的每条消息中包含的信息的平均量。信息量就代表了消息的不确定性。就像上面的荒野求生的例子,比较不可能发生的事情发生了,会给人跟多的信息量。另一个理解是,我要你最大努力猜测下一个事件,熵是你可能猜错的一种度量,或者说熵就是猜测错误导致你有多么”伤不起“。你越有可能出错,来的消息越有价值。
信息熵计算举例
继续来看一个更简单的抛硬币的例子来说明信息熵的取值。如果是一枚正常的硬币做抛硬币实验,你有多大可能猜错正反呢?$1/2$是吧。如果双面完全一样的硬币呢?你没有可能猜错。你说哪个抛硬币实验的信息熵大?带入公式看看:
- 抛正常硬币,只有正反两种可能性,可知 $n=2$。正常硬币,正反概率都是 $1/2$。
- 抛双面相同硬币,只有一种可能,可知 $n=1$,其概率肯定为 1。
实际的情况,肯定是介于两种极端情况之间的。
信息增益
信息增益就是在某个条件下,信息熵减少的程度。通俗点说,就是我告诉你一个秘密,能解决你多大的疑问。
在荒野求生例子中,每个答案看做一个秘密。信息增益当然是悦来客栈门口最大了。
下面理解下公式
\[\displaystyle IG(T,a)=\mathrm {H} {(T)}-\mathrm {H} {(T|a)}\]| $a$ 就是那个求救信息,这个信息让搜索范围缩小了,将上面公式中的 $ | a$ 看做在因为 $a$ 而缩小的空间 |
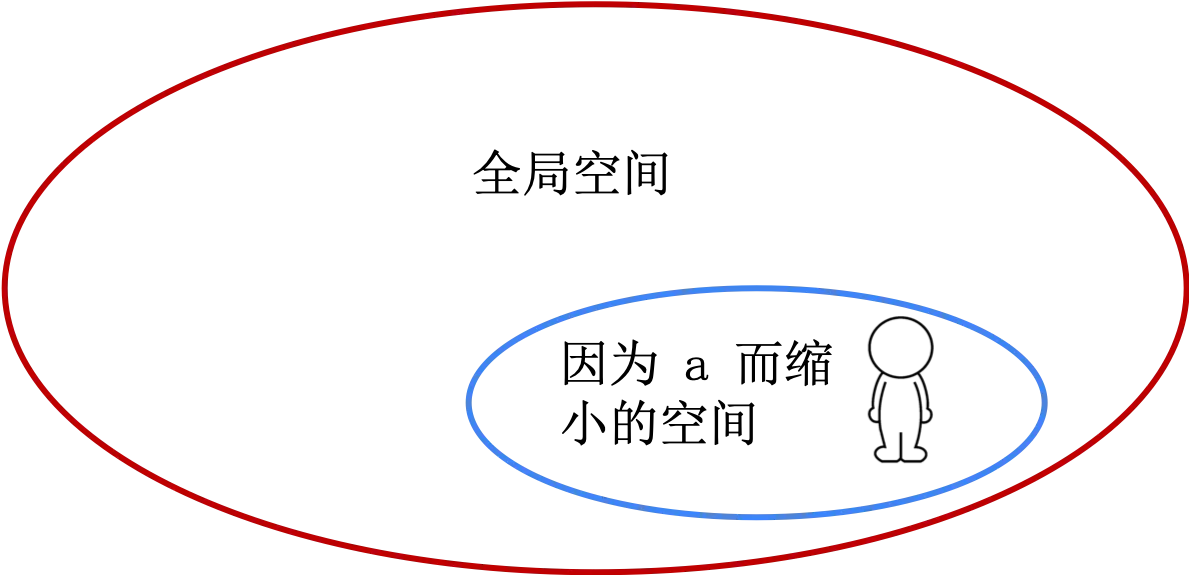
有了这层理解,上面公式就是将你限定在某个更小范围的话,能增大多大的信息量
使用信息熵建立树
其步骤为:
- 计算数据的信息熵
- 计算每一个特征分类之后的信息熵
- 计算此特征每个取值情况下的信息熵
- 计算这些信息熵的加权平均(期望)
- 计算此特征的信息增益
- 使用带来最大信息增益的特征作为根节点,此特征的不同取值作为树枝
- 使用其他特征继续
- 如果分无可分了(都一样或者特征用完了)就停止。
CART 算法决定什么是最好
使用基尼不纯度来为衡量标准,所以我们先看看基尼系数是什么。
基尼不纯度
基尼系数(Gini Coefficient,Gini Index)大家应该都在新闻里听说过,是判断年收入分配公平程度的指标。但是基尼不纯度(Gini Impurity)不是基尼系数,它是另外一个相关但是不同的东西
大量中文和外文的文件将基尼系数和基尼不纯度搞混,大家一定注意。应为维基百科甚至在“Gini impurity”内容备注了“Not to be confused with Gini coefficient.” ,可见二者混淆的严重程度。
基尼不纯度简单来说就是尽最大努力猜的话有多大可能会猜错。准确来说,从一个集合中随机抽抽样一个元素,然后按照标签的分布情况随机打一个标签,基尼不纯度是标记错误程度的度量。
是不是好像和信息熵的意思一样?
比较一下公式:
\[\textit{Gini}: \mathit{Gini}(E) = 1 - \sum_{j=1}^{c}p_j^2 \\ \textit{Entropy}: H(E) = -\sum_{j=1}^{c}p_j\log p_j\]公式也基本一样吧?事实上,使用哪个作为错误程度的衡量标准也没有太大的影响。
使用基尼不纯度构建树
其步骤与信息熵相同,为:
- 计算数据的基尼不纯度
- 计算每一个特征分类之后的基尼不纯度
- 计算此特征每个取值情况下的基尼不纯度
- 计算这些基尼不纯度的加权平均(期望)
- 计算此特征的基尼增益
- 使用带来最大基尼增益的特征作为根节点,此特征的不同取值作为树枝
- 使用其他特征继续
- 如果分无可分了(都一样或者特征用完了)就停止。
CART 和 ID3 最大的区别就是使用了不同的指标进行分类。另一个就是 ID3 只能用于分类问题,而 CART 顾名思义,既可以分类又可以回归。
反馈问题
文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈
点我反馈进入反馈页面不知道如何反馈, 请点击这里