TensorFlow 游乐场(TensorFlow Playground)

使用 TensorFlow Playground 学习深度学习

功能

TensorFlow游乐场是一个通过网页浏览器就可以训练的简单神经网络并实现了可视化训练过程的工具。

界面

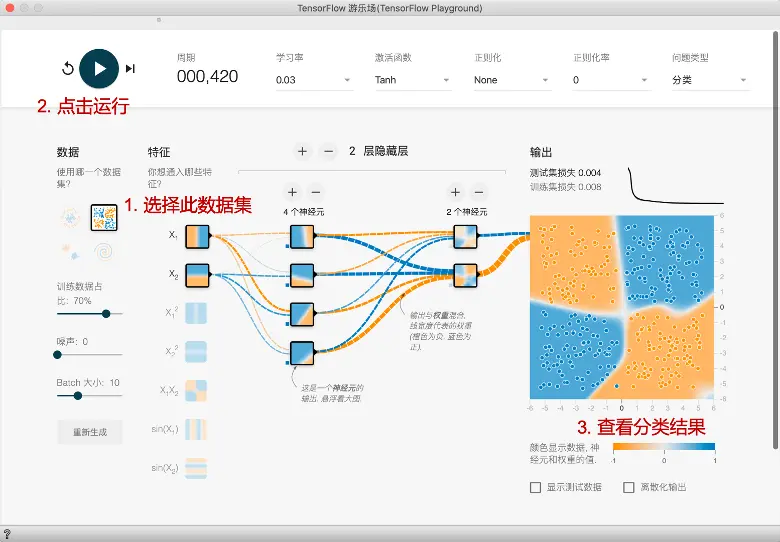
  1. 选择数据集
  2. 运行
  3. 查看分类结果
  • 周期: 训练次数。
  • 学习率: 一个超参数，在梯度下降算法中会用到；学习率是人为根据实际情况来设定
  • 激活函数:默认为非线性函数Tanh；对于线性分类问题可以不使用激活函数
  • 正则化: 正则化方法
  • 正则化率
  • 问题类型:分类还是回归
  • 数据: 数据集类型. 这里提供了四种数据集，我们默认选中第一种；被选中的数据也会显示在最右侧的输出中；在这个数据中，我们可以看到二维平面上有蓝色和黄色的小点；每一个小点代表一个样本；点的颜色代表样本的标签；因为只有两种颜色，所以这里是一个二分类问题
  • 特征向量: 神经网络的输入
  • 隐藏层: 在输入和输出之间的神经网络称为隐藏层；一般神经网络的隐藏层越多这个神经网络越深
  • 输出: 训练结果展示

颜色代表什么

在整个可视化过程中，橙色和蓝色的使用方式略有不同，但通常橙色显示负值，而蓝色显示正值。

数据点（用小圆圈表示）最初是橙色或蓝色，分别对应于正数1和负数1。

在隐藏层中，这些线由神经元之间的连接权重来着色。 蓝色显示正权重，这表示网络正在使用给定的神经元输出。 橙色线表示网络辅助负重。

在输出层中，根据点的原始值将其染成橙色或蓝色。 背景颜色显示网络对特定区域的预测。 颜色的强度表明预测的可信度。

示例

参考

首个神经网络

在本练习中，我们将训练首个小型神经网络。借助神经网络，我们无需使用显式特征组合，便可学习非线性模型。

重要设置如图所示:

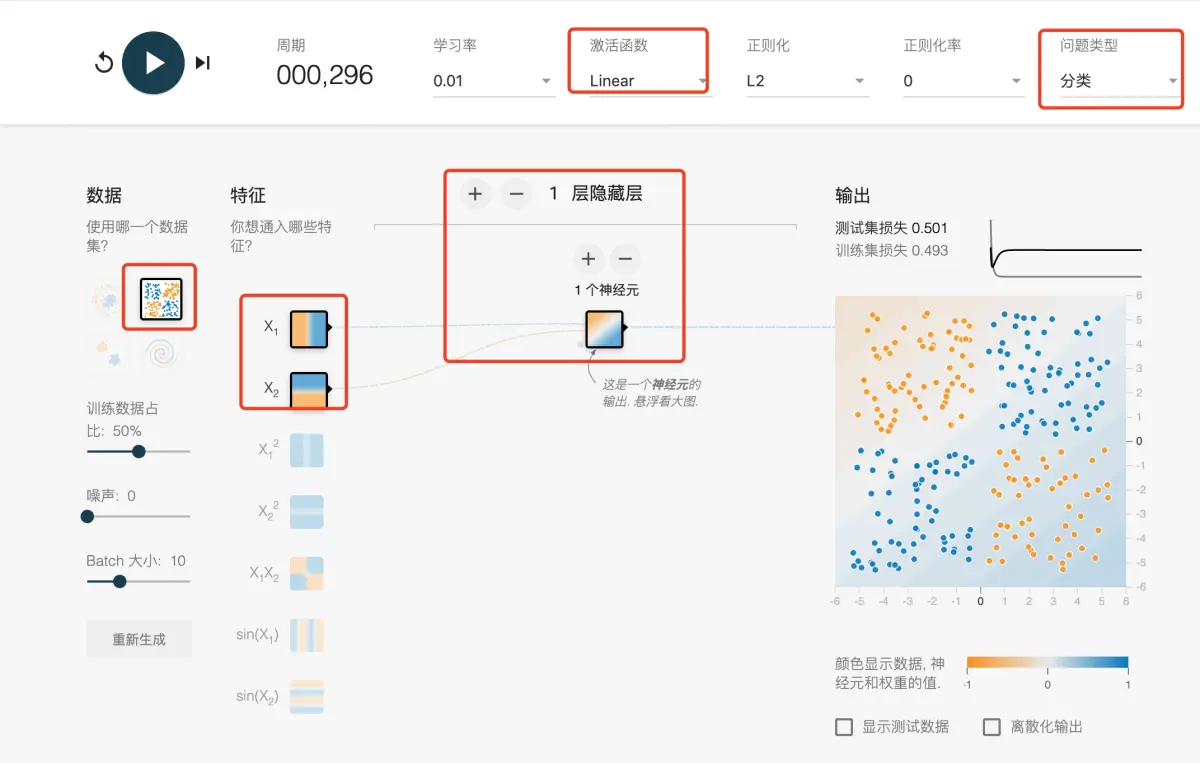
  • 任务 1：给定模型将两个输入特征合并为一个神经元。此模型会学习任何非线性规律吗？运行该模型，以确认您的猜测是否正确。

  • 任务 2：尝试将隐藏层中神经元的数量从 1 增加到 2，此外，尝试将线性激活更改为非线性激活（例如 ReLU）。您能否创建可以学习非线性的模型？

  • 任务 3：通过添加或移除隐藏层和每层的神经元，继续进行实验。此外，您可以随时更改学习速率、正则化和其他学习设置。要使测试损失不超过 0.177，您可以使用的最少节点和层数是多少？

查看任务 1 答案

激活已设为线性，因此，此模型无法学习任何非线性。损失会非常大。

查看任务 2 答案 非线性激活函数可以学习非线性模型。不过，如果一个隐藏层具有 2 个神经元，则学习此模型需要一些时间. 这些练习具有不确定性，因此，有些运行不会学习有效模型，而另一些运行则会完成得很不错
查看任务 3 答案 Playground 的不确定性这一特性在本练习中有所体现。 有些运行包含 3 个按如下方式排列的隐藏层，它们产生的测试损失非常小：
  • 第一层有 3 个神经元。
  • 第二层有 3 个神经元。
  • 第三层有 2 个神经元。
    • 但是，另一些具有相同配置的运行产生的损失却非常大。

    神经网络初始化

    本练习将使用 XOR 数据，用于研究训练神经网络的重复性以及初始化的重要性。

    如图设置, 并且适量加入一些噪声点:

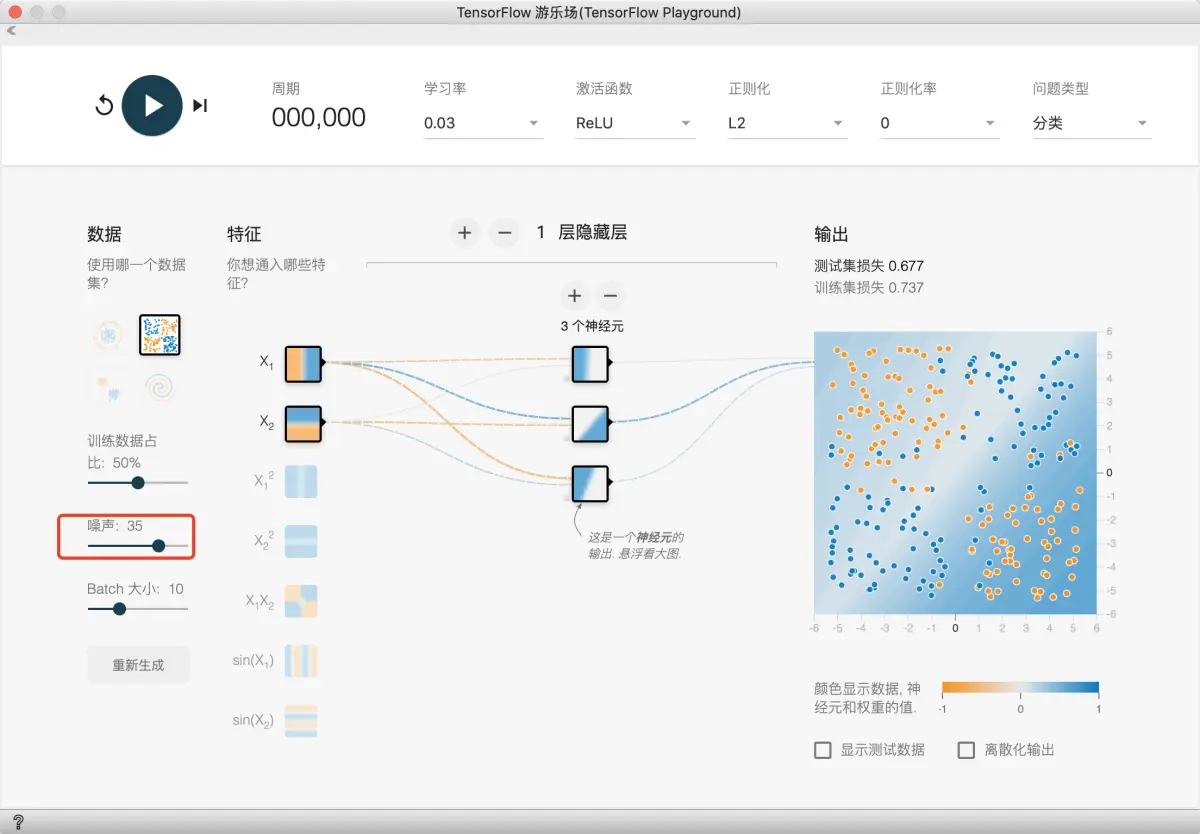
    • 任务 1：运行给定模型四到五次。在每次试验开始之前，请点击重置网络按钮，以获取新的随机初始化数据。（重置网络按钮是一个圆形重置箭头，位于“播放”按钮左侧）。让每次试验至少运行 500 步，以确保图形能收敛。每个模型输出会收敛为何种形状？对于初始化在非凸优化中发挥的作用，这说明了什么？

    • 任务 2：尝试添加一层和几个额外节点，让模型变得稍微复杂点。重复任务 1 的试验。这是否可以提高结果的稳定性？

    查看任务 1 答案 每次运行时，学习模型形成不同的形状。收敛的测试损失各不相同，最低值和最高值几乎相差两倍。
    查看任务 2 答案 添加层和额外节点会产生更多重复的值。每次运行时，生成的模型看起来大致相同。此外，每次运行产生的收敛的测试损失表现出了较小的差异。

    神经网络螺旋

    此数据集是一种混乱的螺旋。显然，线性模型不适用于此处，但即使手动定义的特征组合可能也很难构建。

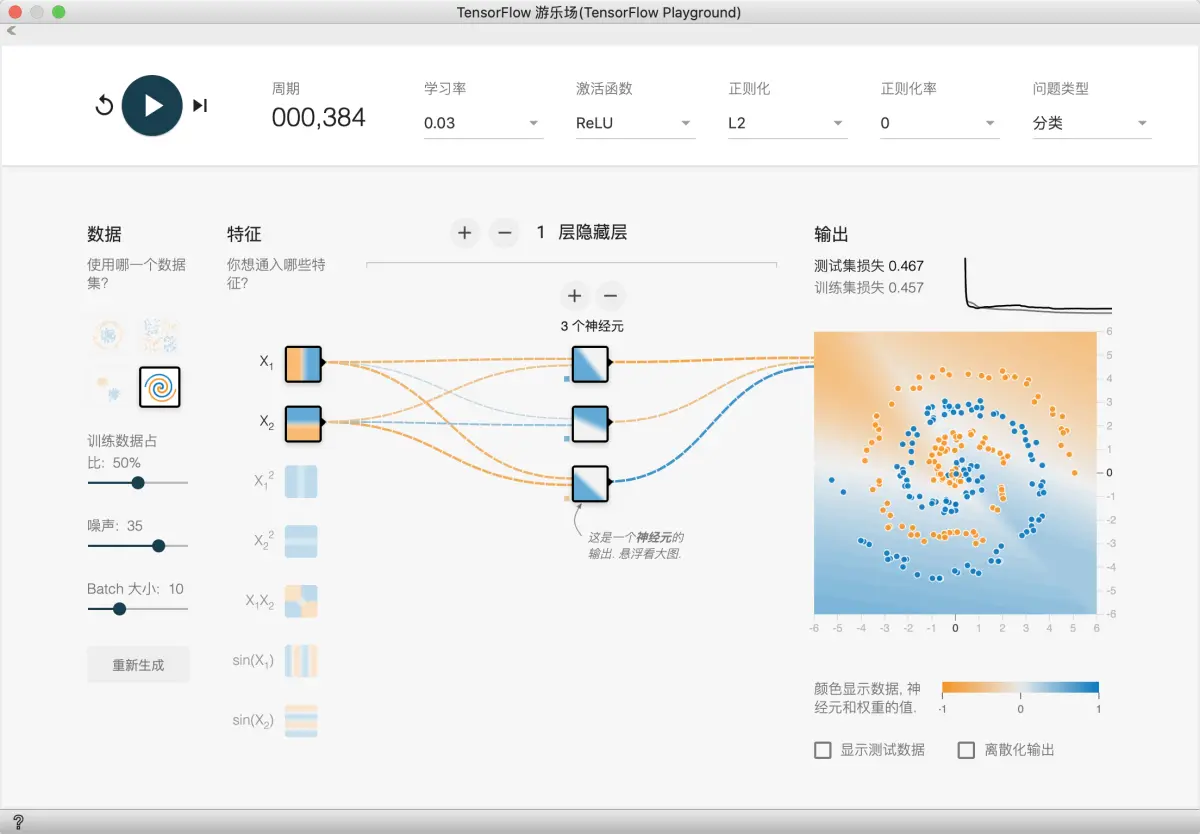
    • 任务 1：只使用 X1 和 X2 训练您可以获得的最佳模型。您可以随时添加或移除层和神经元，以及更改学习速率、正则化率和批量大小等学习设置。您可以获得的最佳测试损失是多少？此模型输出表面的平滑程度如何？

    • 任务 2：即使使用神经网络，通常也需要一些特征工程，才能获得最佳性能。尝试添加额外向量积特征或 sin(X1) 和 sin(X2) 等其他转换。您是否获得了更好的模型？模型输出表面是否更平滑？

    此问题较为复杂, 我们慢慢来.

    首先, 我们试试简单粗暴的方法, 使劲加隐藏层和神经元.

    • 海量神经元

    可以发现, 这个方法第一个特点就是计算量大, 很慢. 而且由于神经元过多, 模型可解释性变差. 经过大量训练后, 损失函数还是不平稳, 波动很大, 运气好的话就能看到好点的结果. 所以说不是神经元越多就越好的.

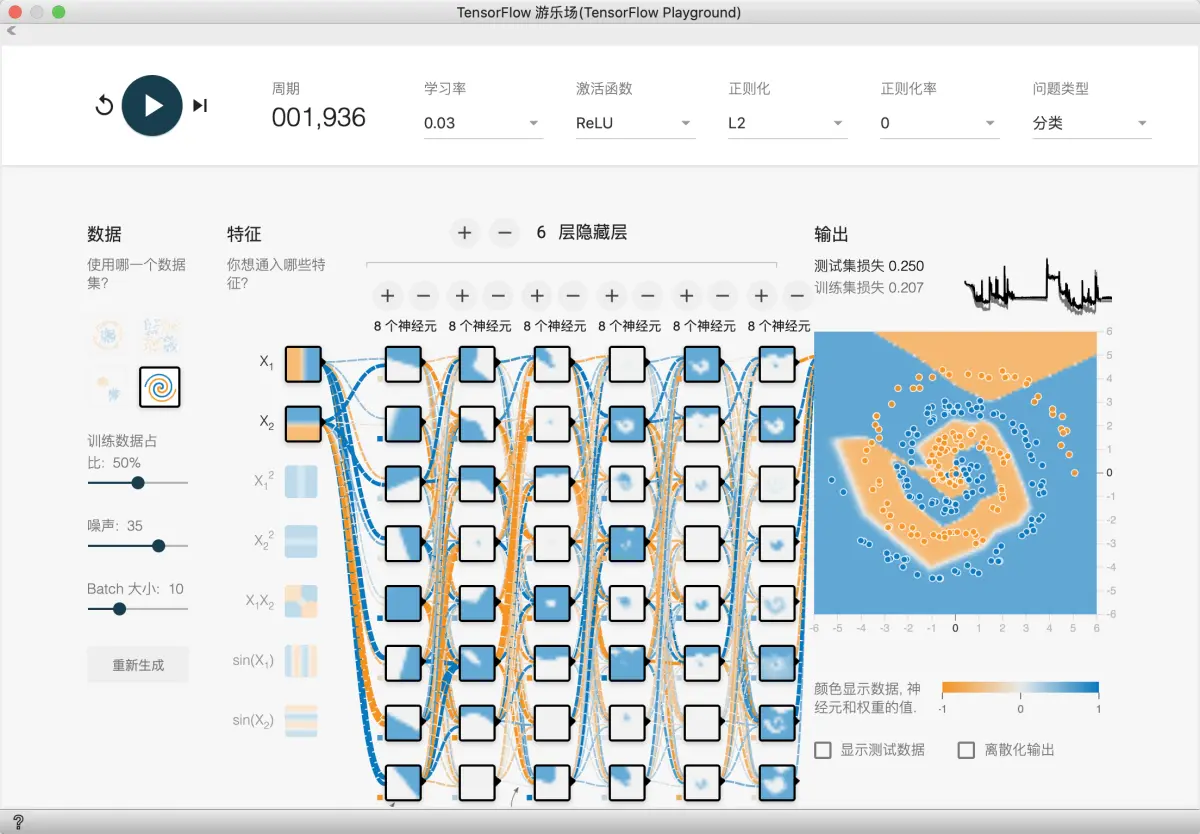
    接下来, 我们试试能否减少神经元数量, 从而更快速训练模型, 得到更好的模型. 并且降低训练学习率, 从而得到更平滑的损失函数值.

    • 降低学习率
    • 无正则化
    • 增大噪声以更明显看出此缺点

    一定时间后, 我们发现已经可以拟合的不错了, 但是损失函数有很多尖峰, 还是不稳定.

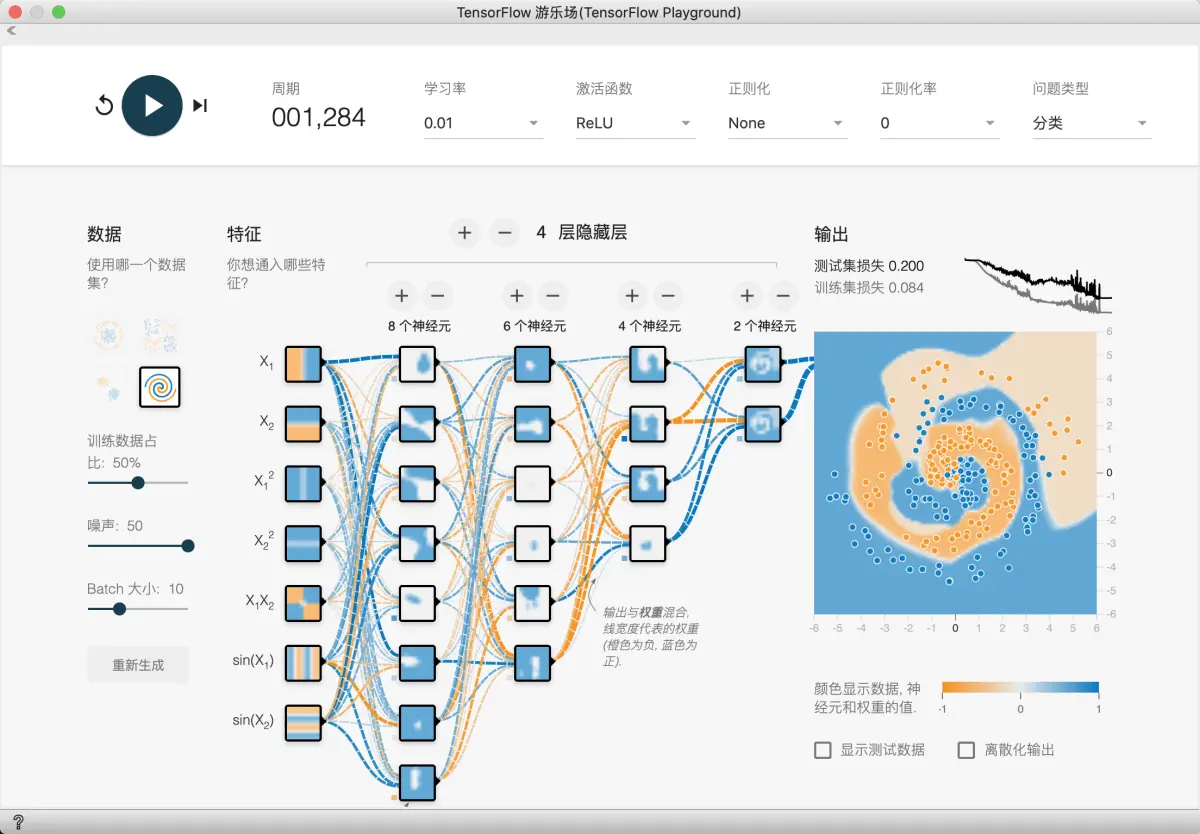
    这说明我们需要更稳定的模型, 所以我们要采取正则化技术

    • 采用正则化

    采用正则化之后, 我们发现尖峰问题有了明显好转

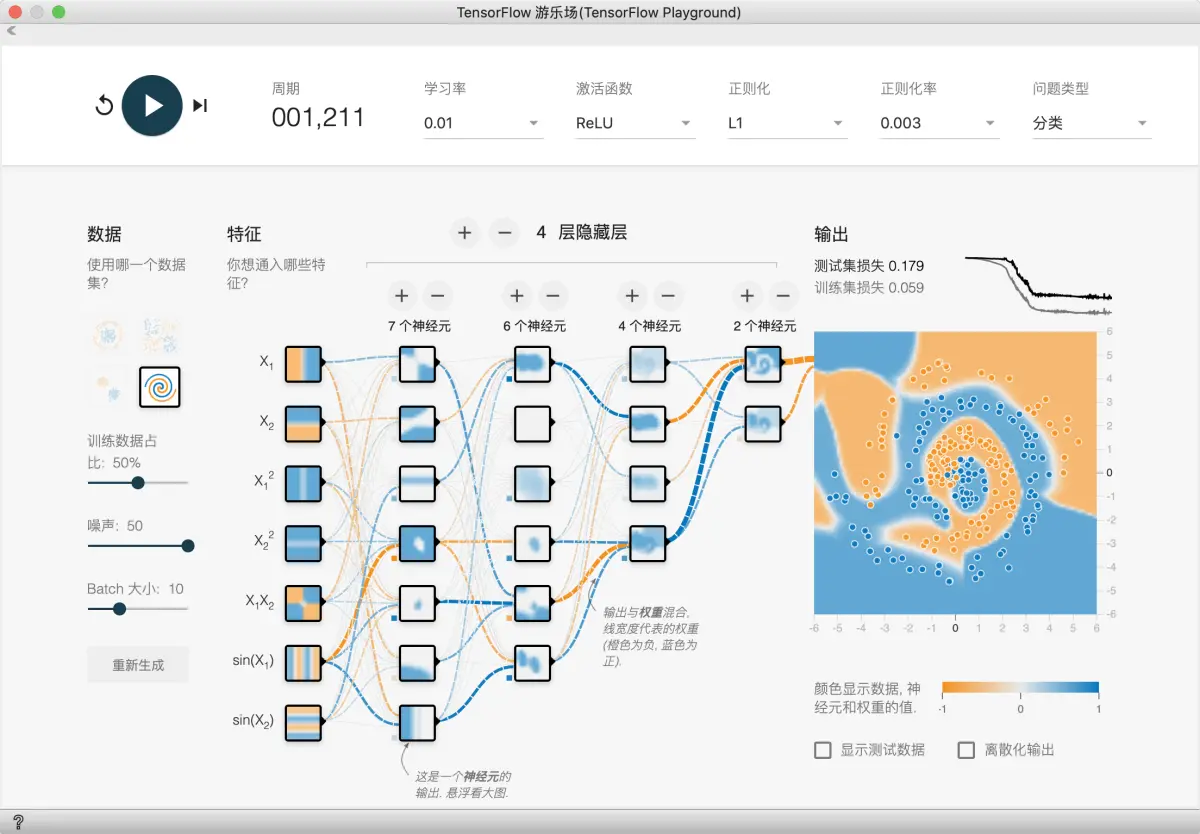
    我们可以试试更多的正则化方法和参数

    最后, 我们也可以试试如果有更合适的特征, 更少的隐藏层和神经元是不是可以得到好的结果.

    反馈问题

    文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

    点我反馈

    进入反馈页面不知道如何反馈, 请点击这里

    更新时间: