多维尺度分析(MDS)
多维尺度分析(MDS)将数据投影到点之间给定距离的平面上
输入
- 数据:输入数据集
- 距离:距离矩阵
- 数据子集:实例的子集
输出
- 选定数据:从图中选择的实例
- 数据:具有 MDS 坐标的数据集
功能
多维尺度分析可找到点的低维(在我们的情况下为二维)投影,并尝试将点之间的距离拟合地尽可能好。由于数据是高维的,或者距离不是欧几里得的,因此通常无法获得完美的拟合。
在输入,小部件需要数据集或距离矩阵。当可视化行之间的距离时,还可以调整点的颜色,更改其形状,对其进行标记并在选择后输出它们。
该算法在对物理模型的模拟中以迭代方式移动这些点:如果两个点彼此之间太近(或太远),就会有力将它们分开(或一起)。 该点在每个时间间隔的变化对应于作用在其上的力的总和。
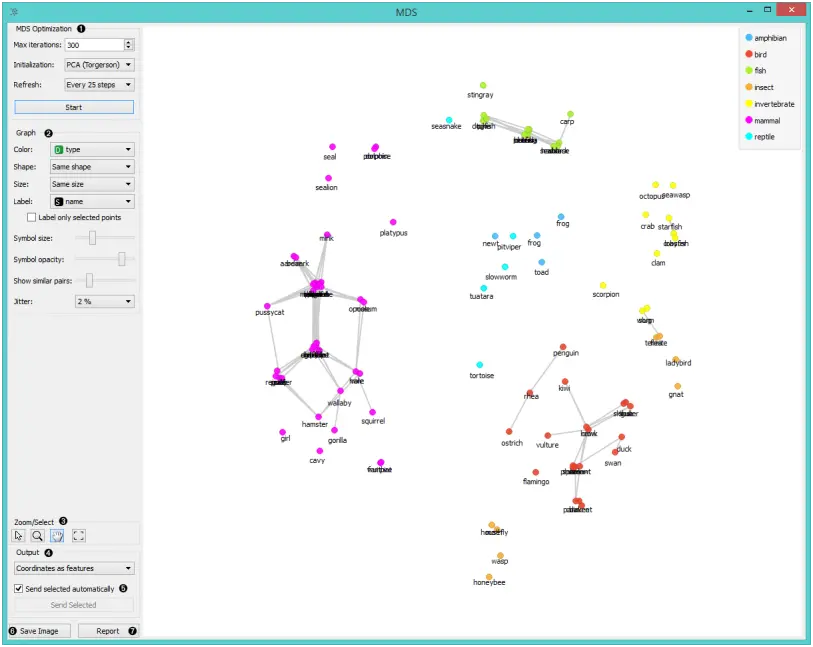
- 小部件在优化期间重新绘制投影。 最优化会在开始时自动运行,之后可以按开始。 -刷新:设置刷新可视化效果的频率。 它可以是“每次迭代”,“每5/10/25/50步”或“从不”(“无”)。设置较低的刷新间隔可使动画更具视觉吸引力,但如果点数较多,则动画速度可能会变慢。
- 可视化选项. 这些选项只在可视化行的时候有效. (在距离(Distances) 选择).
- 如果 自动发送 已打开,则数据子集会自动进行通信,否则您需要按 发送所选。
- 如果要将创建的图像保存到计算机,请按 保存图像。
- 生成报告
示例
上面的图形是使用以下简单模式绘制的。 我们用了 iris.tab 数据集。 使用距离(Distances)小部件,我们将距离矩阵输入 多维尺度分析(MDS) 小部件,我们可以在其中看到 Irisx 显示在二维平面。我们可以在数据表(Data Table) 中看到附加的坐标。
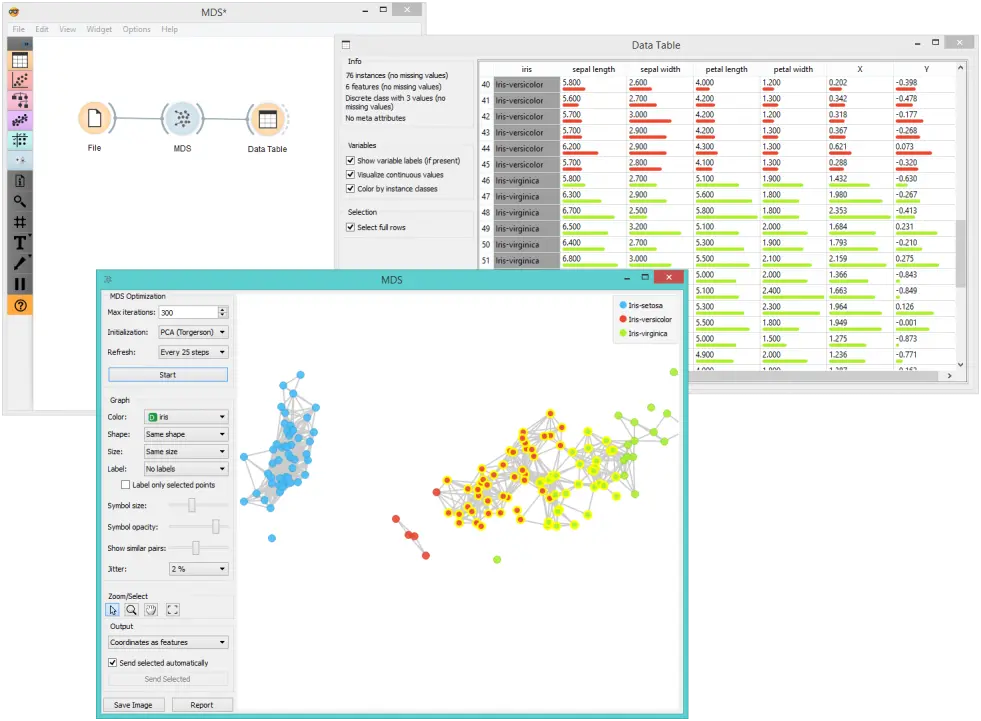
参考文献
Wickelmaier, F. (2003). An Introduction to MDS. Sound Quality Research Unit, Aalborg University. Available here.
反馈问题
文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈
点我反馈进入反馈页面不知道如何反馈, 请点击这里