主成分分析(PCA)
输入数据的 PCA 线性转换。
输入
- 数据:输入数据集
输出
- 转换后的数据:PCA 转换后的数据
- 成分: 特征向量.
功能
主成分分析(PCA)计算输入数据的 PCA 线性变换。它输出具有单个实例权重或主成分权重的转换数据集。
界面
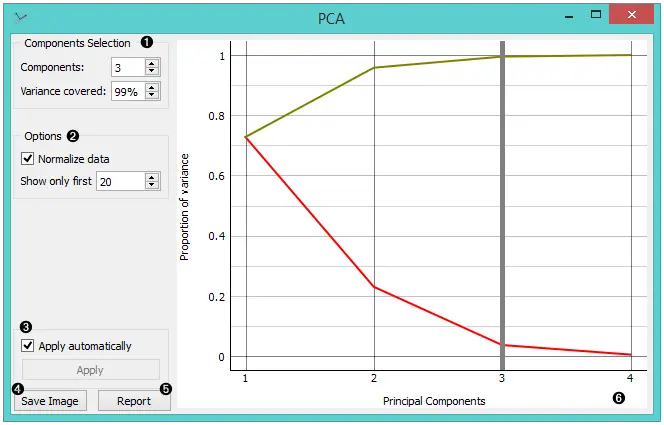
- 选择希望在输出中有多少个主成分。最好选择尽可能少的变量,并尽可能覆盖最大的方差。您还可以设置希望涵盖的主要成分差异。
- 您可以标准化数据以将值调整为通用比例。
- 勾选 自动应用 时,小组件将自动传达所有更改。 或者,单击应用。
- 如果要将创建的图像保存到计算机,请按保存图像。
- 生成报告。
- 主成分图,其中红色(下方)线是每个成分覆盖的方差,绿色(上方)线是成分覆盖的累积方差。
可以在 “组件选择” 输入框中或通过拖动图形中的垂直截止线来选择转换的成分数。
示例
主成分分析(PCA) 可用于简化大型数据集的可视化。下面,我们使用 Iris 数据集来展示如何使用PCA 改善数据集的可视化。与默认设置相比,散点图(Scatter Plot)中转换后的数据在类别之间显示出更加清晰的区别。
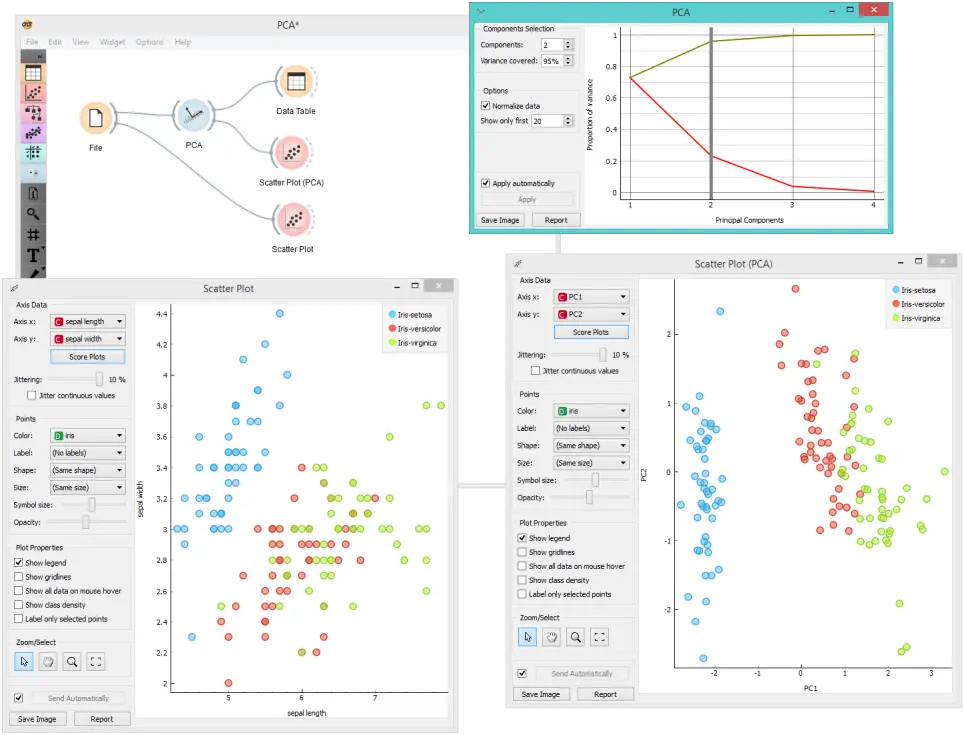
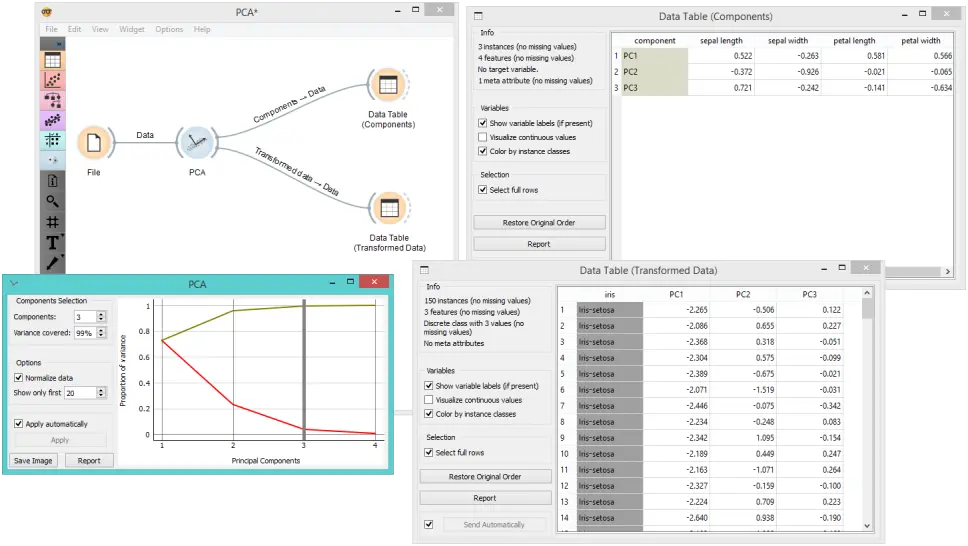
该小部件提供两个输出:转换后的数据和主要成分。转换后的数据是新坐标系中各个实例的权重,而成分是系统描述符(主要成分的权重)。 当输入数据表(Data Table)时,我们可以看到两个数字形式的输出。 我们使用了两个数据表,以提供工作流程的更清晰的可视化,但是您也可以选择编辑链接,以便仅在一个数据表中显示数据。 您只需要创建两个链接,然后将转换后的数据和成分输入连接到数据 输出即可。
反馈问题
文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈
点我反馈进入反馈页面不知道如何反馈, 请点击这里