随机梯度下降(Stochastic Gradient Descent)

使用梯度下降的随机逼近最小化目标函数。

输入

  • 数据：输入数据集
  • 预处理器：预处理方法

输出

  • 学习器：随机梯度下降学习算法
  • 模型：训练过的模

功能

随机梯度下降(Stochastic Gradient Descent) 小部件使用随机梯度下降，该函数通过线性函数将所选损失函数最小化。该算法通过一次考虑一个样本来逼近真实梯度，并同时基于损失函数的梯度更新模型。为了进行回归，它将预测变量作为总和的最小化变量（即M估计量）返回，对于大规模和稀疏数据集特别有用。

界面

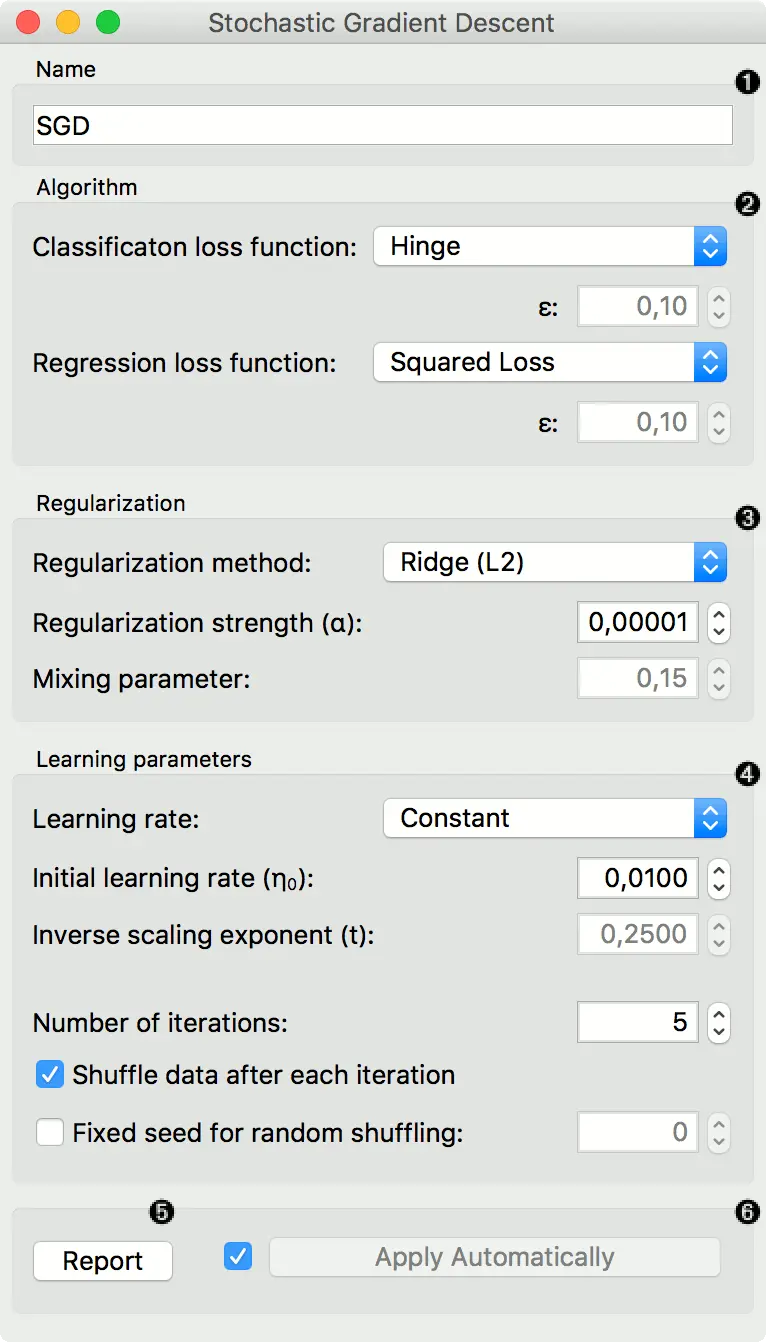
  1. 指定模型名称。 默认名称为“SGD”。
  2. 算法参数：
    • 分类损失函数：
      • Hinge (linear SVM)
      • Logistic Regression (logistic regression SGD)
      • Modified Huber (smooth loss that brings tolerance to outliers as well as probability estimates)
      • Squared Hinge (quadratically penalized hinge)
      • Perceptron (linear loss used by the perceptron algorithm)
      • Squared Loss (fitted to ordinary least-squares)
      • Huber (switches to linear loss beyond ε)
      • Epsilon insensitive (ignores errors within ε, linear beyond it)
      • Squared epsilon insensitive (loss is squared beyond ε-region).
    • 回归损失函数:
      • Squared Loss (fitted to ordinary least-squares)
      • Huber (switches to linear loss beyond ε)
      • Epsilon insensitive (ignores errors within ε, linear beyond it)
      • Squared epsilon insensitive (loss is squared beyond ε-region).
  3. 正则化规范以防止过度拟合:

    正则化强度定义将应用多少正则化（我们进行正则化越少，我们允许模型拟合数据的程度就越多）以及混合参数（L1 和 L2 损失之间的比率将是多少）（如果设置为 0，则损失为 L2 ，如果设置为 1，则为 L1）。

  4. 学习参数.
    • 学习率:
      • 常数: learning rate stays the same through all epochs (passes)
      • 最优的: a heuristic proposed by Leon Bottou
      • 反比例: earning rate is inversely related to the number of iterations
    • 初始学习率。
    • 反比例指数：学习速率衰减。
    • 迭代次数：通过训练数据的次数。
    • 如果启用在每次迭代后随机化数据，则每次通过后都会混排数据实例的顺序。
    • 如果固定随机化种子处于启用状态，则该算法将使用固定的随机种子并允许复制结果。
  5. 发送报告
  6. 勾选 “自动应用” 以自动传送对其他小部件的更改，并在连接学习数据后立即训练分类器。 或者，在配置后按 “应用”。

示例

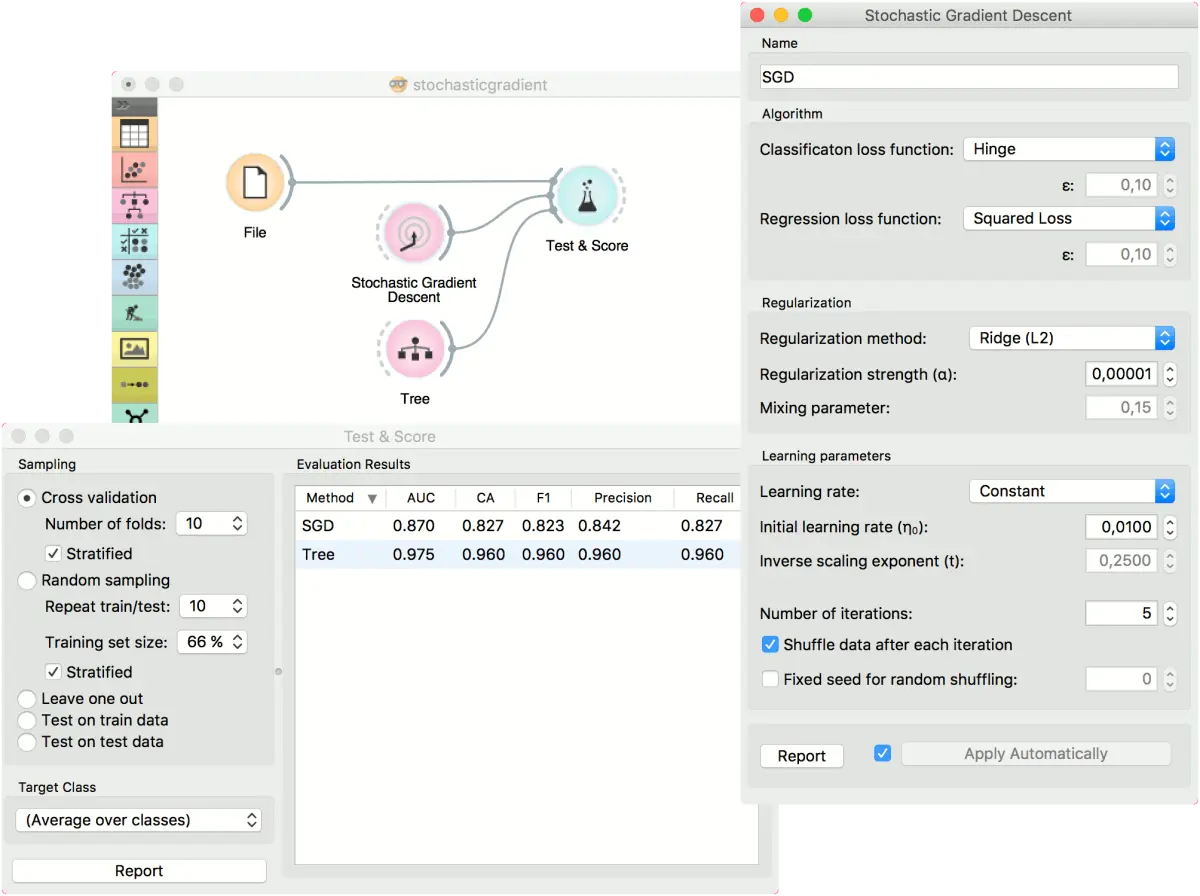
对于分类任务，我们将使用 iris 数据集并在其上测试两个模型。 我们将 随机梯度下降(Stochastic Gradient Descent) 和树(Tree) 连接到测试与评分(Test & Score)。 我们还将文件(File) 连接到 测试与评分(Test & Score)，并在小部件中观察了模型的性能。

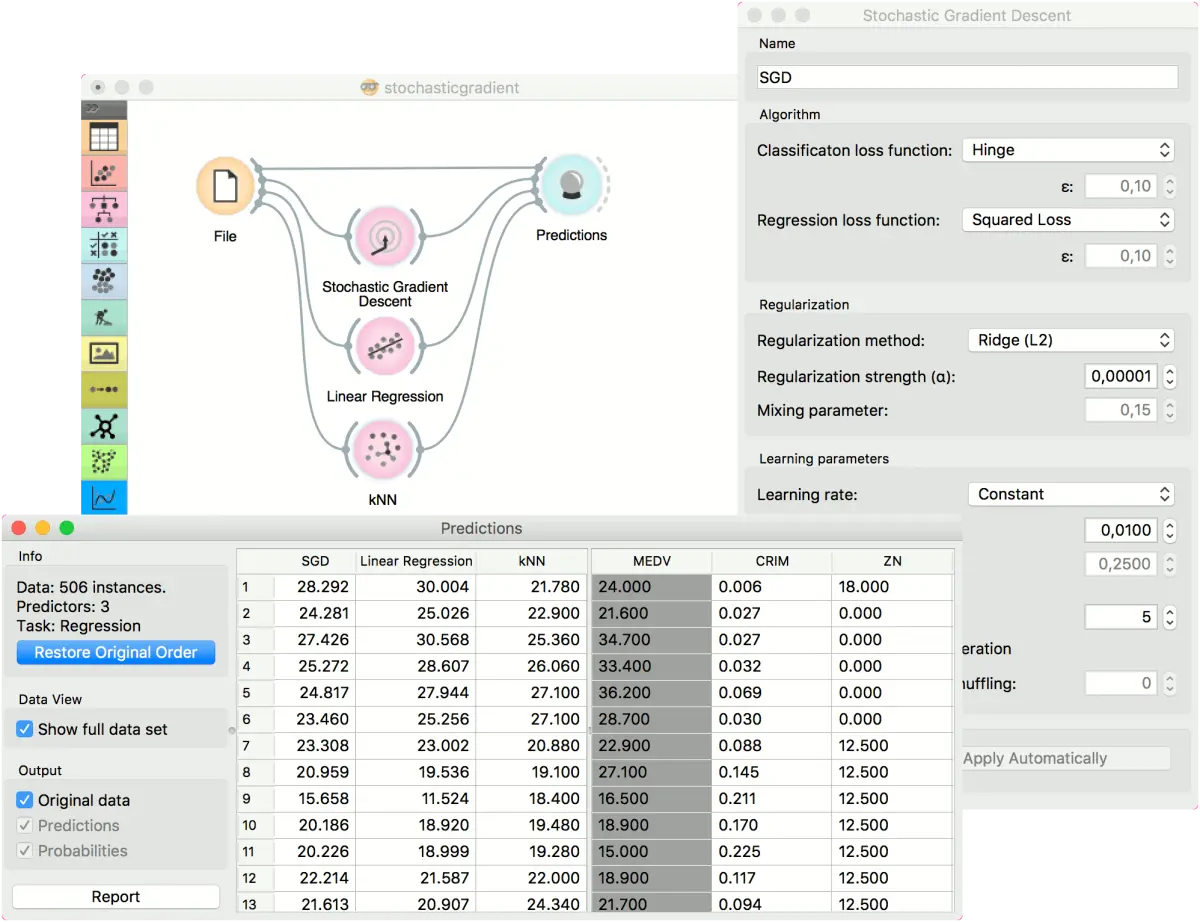
对于回归任务，我们将比较三种不同的模型，以查看预测哪种结果。出于本示例的目的，使用了 housing 数据集。 我们将 文件(File) 连接到 随机梯度下降(Stochastic Gradient Descent) ，线性回归(Linear Regression) 和k 近邻(kNN) 小部件，然后将全部四个添加到预测(Predictions) 小部件。

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里

更新时间: