k 均值(k-Means)

使用 k 均值聚类算法对项目进行分组。

输入

  • 数据: 输入数据

输出

  • 数据：以聚类索引为类别属性的数据集

功能

该小部件将k-Means聚类算法应用于数据，并输出一个新的数据集，其中将聚类索引用作类别属性。原始的类别属性（如果存在）将移至元属性。小部件中还显示了各种 k 的聚类结果得分。

界面

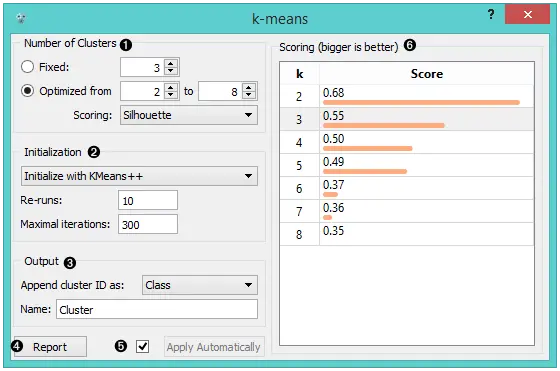
  1. 选择聚类(簇)数。
    • 固定：算法将数据聚类到指定数量的聚类中。
    • 优化：小部件显示所选聚类范围的聚类得分：
  2. 选择初始化方法（算法开始聚类的方式）：
    • k-Means++: 第一个中心是随机选择的，随后从其余点中选择，其概率与距最近点的平方距离成正比
    • 随机初始化: 聚类首先被随机分配，然后通过进一步的迭代进行更新
    • 重新运行: 从随机初始位置运行算法多少次；将使用簇内平方和最低的结果
    • 最大迭代次数: 每个迭代中的最大迭代次数
  3. 小部件输出带有附加集群信息的新数据集。选择如何附加聚类信息（作为类，要素或元属性）并命名该列。
  4. 如果勾选了“自动应用”，则小部件将自动提交更改。 或者，单击应用。
  5. 生成报告。
  6. 检查各种k的聚类结果分数。

示例

使用如下工作流演示:

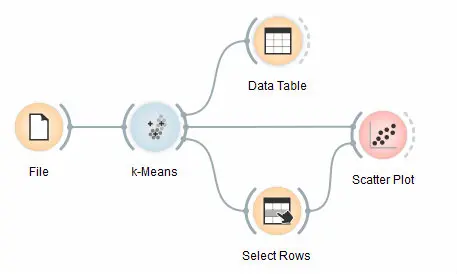
首先，我们加载 Iris 数据集，将其分为三个簇，并在数据表(Data Table)中显示，可以观察到哪个实例进入了哪个簇。有趣的部分是散点图(Scatter Plot)和选择行(Select Rows)。

由于 k均值(k-Means) 将聚类索引添加为类别属性，因此散点图将根据它们所在的聚类为点着色。

我们真正感兴趣的是由（无监督）聚类算法推导的聚类与数据中的实际类别匹配的程度。因此，我们使用选择行(Select Rows) 小部件，在其中可以选择各个类别并在散点图(Scatter Plot)中标记相应的点。 setosa 完美的匹配，而其他两个类别也不错。

您可能已经注意到，我们未选中 选择行(Select Rows) 中的 “删除未使用的值/属性” 和 “删除未使用的分类”。 这很重要：如果小部件修改了属性，它将输出已修改实例的列表，并且 散点图(Scatter Plot)]散点图无法将它们与原始数据进行比较。

测试聚类和原始类别之间的匹配的一种更简单的方法可能是使用分布(Distributions)小部件。

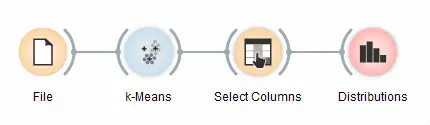
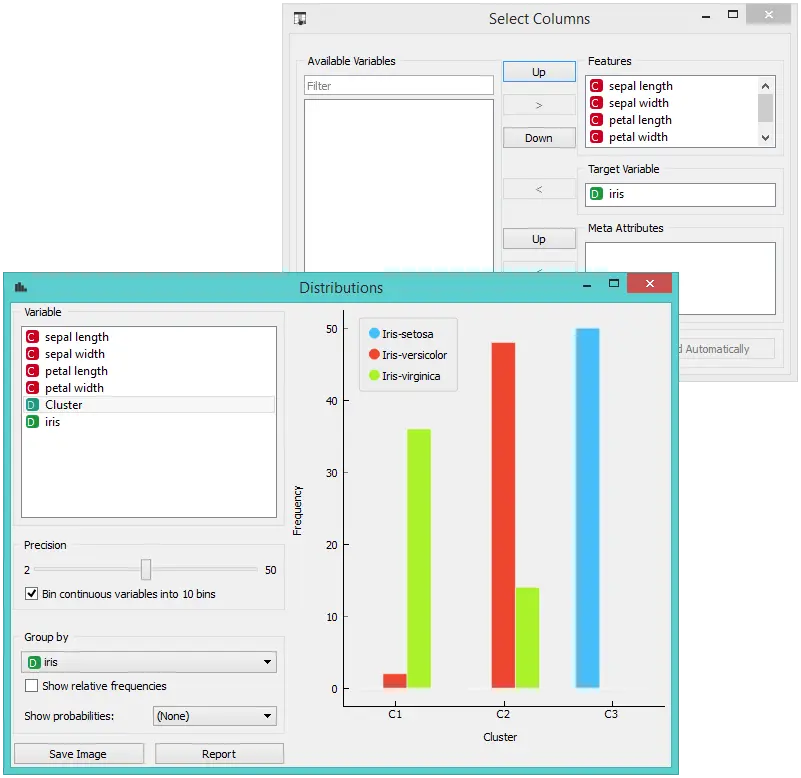
唯一但是不重要的问题是此小部件仅可视化常规而非元属性。我们通过使用选择列(Select Columns)解决此问题：我们将原始分类 Iris 恢复为分类，并将簇索引放在属性。

setosa 的匹配很完美：setosa 的所有实例都位于第三个簇中（蓝色）。48 个 versicolors 位于第二个簇（红色）中，而两个则位于第一个簇中。 对于 virginicae，第一个簇为 36 个，第二个簇为 14 个。

反馈问题

文档有问题? 或者有其他意见和建议? 请在本文档的 Github 仓库直接反馈

点我反馈

进入反馈页面不知道如何反馈, 请点击这里

更新时间: